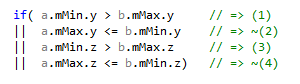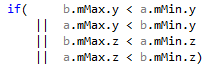Box pruning revisited - part 11 - the last branch
Tuesday, February 14th, 2017Part 11 – the last branch
The SIMD version gave us a good speedup. The best scalar version was also quite successful, thanks to the removal of several hard-to-predict branches.
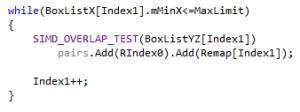
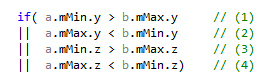
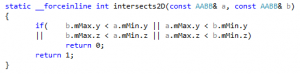
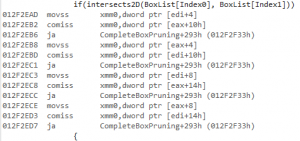
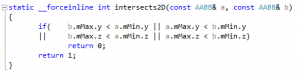
Looking at the remaining code with this in mind, one more branch jumps to the eyes, just before the SIMD overlap test:
This ensures that we never test a box against itself, but I don’t quite remember why it’s there. The way the code is written, it cannot happen. So this test can just be removed. Since it never happens, the branch is likely to be always correctly predicted, and thus the expected gains are small, if any.
But still, worth doing - it’s just one line.
And the results are actually interesting:
Home PC:
Unsafe version:
Complete test (brute force): found 11811 intersections in 781447 K-cycles.
15224 K-cycles.
14386 K-cycles.
14633 K-cycles.
14387 K-cycles.
14376 K-cycles.
14392 K-cycles.
14376 K-cycles.
14373 K-cycles.
14579 K-cycles.
14400 K-cycles.
14374 K-cycles.
14388 K-cycles.
14373 K-cycles.
14372 K-cycles.
14471 K-cycles.
14404 K-cycles.
Complete test (box pruning): found 11715 intersections in 14372 K-cycles.
Safe version:
Complete test (brute force): found 11811 intersections in 781701 K-cycles.
15306 K-cycles.
14533 K-cycles.
14513 K-cycles.
14731 K-cycles.
14552 K-cycles.
14512 K-cycles.
14528 K-cycles.
14514 K-cycles.
14514 K-cycles.
14528 K-cycles.
14535 K-cycles.
14513 K-cycles.
14526 K-cycles.
14515 K-cycles.
14515 K-cycles.
14621 K-cycles.
Complete test (box pruning): found 11811 intersections in 14512 K-cycles.
Office PC:
Unsafe version:
Complete test (brute force): found 11811 intersections in 824867 K-cycles.
13618 K-cycles.
12900 K-cycles.
12573 K-cycles.
12957 K-cycles.
12570 K-cycles.
12911 K-cycles.
12572 K-cycles.
12573 K-cycles.
12588 K-cycles.
13153 K-cycles.
13447 K-cycles.
13212 K-cycles.
13429 K-cycles.
13214 K-cycles.
13527 K-cycles.
13229 K-cycles.
Complete test (box pruning): found 11715 intersections in 12570 K-cycles.
Safe version:
Complete test (brute force): found 11811 intersections in 816240 K-cycles.
13227 K-cycles.
13013 K-cycles.
12621 K-cycles.
14329 K-cycles.
12624 K-cycles.
13009 K-cycles.
13533 K-cycles.
13171 K-cycles.
12881 K-cycles.
13181 K-cycles.
13265 K-cycles.
13248 K-cycles.
13245 K-cycles.
13242 K-cycles.
13267 K-cycles.
12611 K-cycles.
Complete test (box pruning): found 11811 intersections in 12611 K-cycles.
The gains are summarized here:
|
Home PC |
Timings (K-Cycles) |
Delta (K-Cycles) |
Speedup |
Overall X factor |
|
(Version1) |
(101662) |
|
|
|
|
Version2 - base |
98822 |
0 |
0% |
1.0 |
|
Version3 |
93138 |
~5600 |
~5% |
~1.06 |
|
Version4 |
81834 |
~11000 |
~12% |
~1.20 |
|
Version5 |
78140 |
~3600 |
~4% |
~1.26 |
|
Version6a |
60579 |
~17000 |
~22% |
~1.63 |
|
Version6b |
41605 |
~18000 |
~31% |
~2.37 |
|
(Version7) |
(40906) |
- |
- |
- |
|
(Version8) |
(31383) |
(~10000) |
(~24%) |
(~3.14) |
|
Version9a |
34486 |
~7100 |
~17% |
~2.86 |
|
Version9b - unsafe |
32477 |
~2000 |
~5% |
~3.04 |
|
Version9b - safe |
32565 |
~1900 |
~5% |
~3.03 |
|
Version9c - unsafe |
16223 |
~16000 |
~50% |
~6.09 |
|
Version9c - safe |
14802 |
~17000 |
~54% |
~6.67 |
|
(Version10) |
(16667) |
- |
- |
- |
|
Version11 - unsafe |
14372 |
~1800 |
~11% |
~6.87 |
|
Version11 - safe |
14512 |
~200 |
~2% |
~6.80 |
|
Office PC |
Timings (K-Cycles) |
Delta (K-Cycles) |
Speedup |
Overall X factor |
|
(Version1) |
(96203) |
|
|
|
|
Version2 - base |
92885 |
0 |
0% |
1.0 |
|
Version3 |
88352 |
~4500 |
~5% |
~1.05 |
|
Version4 |
77156 |
~11000 |
~12% |
~1.20 |
|
Version5 |
73778 |
~3300 |
~4% |
~1.25 |
|
Version6a |
58451 |
~15000 |
~20% |
~1.58 |
|
Version6b |
45634 |
~12000 |
~21% |
~2.03 |
|
(Version7) |
(43987) |
- |
- |
- |
|
(Version8) |
(29083) |
(~16000) |
(~36%) |
(~3.19) |
|
Version9a |
31864 |
~13000 |
~30% |
~2.91 |
|
Version9b - unsafe |
15097 |
~16000 |
~52% |
~6.15 |
|
Version9b - safe |
15116 |
~16000 |
~52% |
~6.14 |
|
Version9c - unsafe |
12707 |
~2300 |
~15% |
~7.30 |
|
Version9c - safe |
12562 |
~2500 |
~16% |
~7.39 |
|
(Version10) |
(15648) |
- |
- |
- |
|
Version11 - unsafe |
12570 |
~100 |
~1% |
~7.38 |
|
Version11 - safe |
12611 |
- |
- |
~7.36 |
Version 11 is compared to version 9c here.
No difference on the office PC, but on the home PC the safe & unsafe versions are suddenly the same speed. Hmmm. We’ll never solve that particular mystery then. Oh well. All is good now at least.
Now what? Are we done?
We are about 7x faster than when we started, which is pretty good!
…but not quite the order of magnitude we wanted to reach.
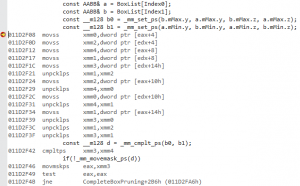
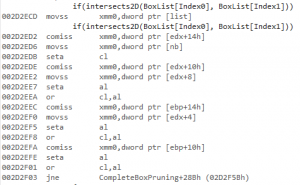
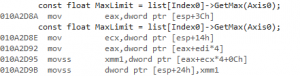
At this point there isn’t much left in the inner loop, at least on the C++ side of things. So let’s check the new disassembly. The inner loop we’re interested in is:
And the corresponding disassembly is simple enough to isolate:
//SIMD_OVERLAP_TEST(BoxListYZ[Index1])
003E2FB3 cmpltps xmm1,xmmword ptr [edi]
003E2FB7 movmskps eax,xmm1
003E2FBA cmp eax,0Ch
003E2FBD jne CompleteBoxPruning+2D1h (03E3011h)
//pairs.Add(RIndex0).Add(Remap[Index1]);
003E2FBF mov eax,dword ptr [esi+4]
003E2FC2 cmp eax,dword ptr [esi]
003E2FC4 jne CompleteBoxPruning+28Fh (03E2FCFh)
003E2FC6 push 1
003E2FC8 mov ecx,esi
003E2FCA call IceCore::Container::Resize (03E1350h)
003E2FCF mov ecx,dword ptr [esi+4]
003E2FD2 mov eax,dword ptr [esi+8]
003E2FD5 mov edx,dword ptr [esp+34h]
003E2FD9 mov dword ptr [eax+ecx*4],edx
003E2FDC inc dword ptr [esi+4]
003E2FDF mov edx,dword ptr [esp+20h]
003E2FE3 mov eax,dword ptr [esi+4]
003E2FE6 mov ecx,dword ptr [edx]
003E2FE8 mov dword ptr [esp+30h],ecx
003E2FEC cmp eax,dword ptr [esi]
003E2FEE jne CompleteBoxPruning+2B9h (03E2FF9h)
003E2FF0 push 1
003E2FF2 mov ecx,esi
003E2FF4 call IceCore::Container::Resize (03E1350h)
003E2FF9 mov ecx,dword ptr [esi+4]
003E2FFC mov eax,dword ptr [esi+8]
003E2FFF mov edx,dword ptr [esp+30h]
003E3003 mov dword ptr [eax+ecx*4],edx
003E3006 inc dword ptr [esi+4]
003E3009 mov ecx,dword ptr [esp+28h]
003E300D mov edx,dword ptr [esp+20h]
// while(BoxListX[Index1].mMinX<=MaxLimit)
003E3011 movss xmm0,dword ptr [esp+38h]
003E3017 movaps xmm1,xmmword ptr [esp+40h]
003E301C add ecx,8
003E301F add edx,4
003E3022 add edi,10h
003E3025 comiss xmm0,dword ptr [ecx]
003E3028 mov dword ptr [esp+20h],edx
003E302C mov dword ptr [esp+28h],ecx
003E3030 jae CompleteBoxPruning+273h (03E2FB3h)
I added two blank lines and color-coded the whole thing to clearly delimitate three blocks of code.
Roughly, the first block is the SIMD overlap test, the second block is for writing the pair indices when an overlap is found, and the last block is the while loop (easily identified by the comiss instruction).
It’s… not great.
Where do I start?
———————
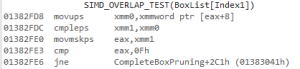
In the first two lines, since the xmmword ptr [edi] is the actual load of BoxListYZ[Index1], writing it this way means that xmm1 contains our constant box for the loop (the preloaded Box0YZ in the C++ code):
003E2FB3 cmpltps xmm1,xmmword ptr [edi]
003E2FB7 movmskps eax,xmm1
But the cmpltps instruction is always going to destroy the contents of xmm1. So this register will need to be reloaded for the next iteration. And indeed, that’s what happens in the third block:
003E3017 movaps xmm1,xmmword ptr [esp+40h]
We also confirm that edi is the BoxListYZ array, thanks to:
003E3022 add edi,10h
10h == 16 == sizeof(SIMD_AABB_YZ), makes sense.
Question 1: why write the code in such a way that it destroys the constant box?
Question 2: why reload the constant box from the stack? Why not keeping it in a register? The whole loop only uses two xmm registers (!) so it’s not like there’s a shortage of them.
———————
In the third block, we have this:
003E301C add ecx,8
And then:
003E3025 comiss xmm0,dword ptr [ecx]
Which means that ecx is the BoxListX array (with sizeof(SIMD_AABB_X)==8), and dword ptr [ecx] (a scalar load) is the assembly for “BoxListX[Index1].mMinX” in the C++ code.
Makes sense.
But then it also means that xmm0 is “MaxLimit“, which gets reloaded just before from the stack:
003E3011 movss xmm0,dword ptr [esp+38h]
Doesn’t make sense.
Question 3: Why do you reload it from the stack each time? It’s a constant for the whole loop. There are free available xmm registers. Just put it in xmm2, keep it there, and the “movss” instruction above just vanishes.
———————
In the third block again, we have this:
003E301F add edx,4
…
003E3028 mov dword ptr [esp+20h],edx
003E302C mov dword ptr [esp+28h],ecx
We saw ecx before, it’s the BoxListX array.
Question 4: why do you push it to the stack? Why don’t you keep it in a register?
———————
Then there’s edx, incremented by 4 and also pushed to the stack. If you look for [esp+20h] to check where we read it again, you find two places:
003E2FDF mov edx,dword ptr [esp+20h]
And:
003E300D mov edx,dword ptr [esp+20h]
The first place happens after the first “push back” call, and corresponds to this C++ code:
Add(Remap[Index1])
The second place happens after the second “push back” call, and simply restores the edx register, which is not actually used when the SIMD-overlap test doesn’t find an overlap.
You guessed it, edx is Index1, or rather Remap[Index1] as you can see from these lines in the second block:
003E2FDF mov edx,dword ptr [esp+20h]
…
003E2FE6 mov ecx,dword ptr [edx]
Right. Ok. But then…
Question 5: why do you save edx to the stack all the time (address 003E3028)? Why don’t you just save and restore it only when an overlap actually occurs?
Question 6: same question for ecx.
———————
As for the second block, it looks fine overall. Still, I know some people will ask this one:
Question 7: why do you use a custom vector class instead of std::vector?
Ok, let’s quickly deal with that one first, it won’t take long. Replace the custom container with std::vector and you get:
Home PC:
Unsafe:
Complete test (brute force): found 11811 intersections in 851569 K-cycles.
19727 K-cycles.
18913 K-cycles.
18881 K-cycles.
18879 K-cycles.
18908 K-cycles.
18901 K-cycles.
18891 K-cycles.
18882 K-cycles.
18878 K-cycles.
19110 K-cycles.
18902 K-cycles.
18901 K-cycles.
18881 K-cycles.
18895 K-cycles.
18904 K-cycles.
18882 K-cycles.
Complete test (box pruning): found 11715 intersections in 18878 K-cycles.
Office PC:
Unsafe:
Complete test (brute force): found 11811 intersections in 888075 K-cycles.
19200 K-cycles.
18307 K-cycles.
18584 K-cycles.
18729 K-cycles.
18306 K-cycles.
18647 K-cycles.
18571 K-cycles.
18306 K-cycles.
18767 K-cycles.
18551 K-cycles.
18420 K-cycles.
18659 K-cycles.
18530 K-cycles.
18365 K-cycles.
18491 K-cycles.
18310 K-cycles.
Complete test (box pruning): found 11715 intersections in 18306 K-cycles.
That is:
|
Home PC |
Timings |
|
Version11 - unsafe - ICE container |
14372 |
|
Version11 - unsafe - std::vector |
18878 |
|
Office PC |
Timings |
|
Version11 - unsafe - ICE container |
12570 |
|
Version11 - unsafe - std::vector |
18306 |
Just look at the numbers. That’s why I’m not using std::vector. It has never been able to implement a simple “push_back” correctly. It’s 2017 and std::vector still cannot match the first basic C++ class I wrote back in 1999.
There is no need to tell me about STLPort or EASTL or whatever: I’ve heard it all. If I cannot rely on the version included with Visual Studio, if I have to switch to some external library, I’d rather use my own. At least I know it’s properly implemented.
Just for “fun”, with the custom container the second block above is about 27 lines of code. Right?
Ok, now take a deep breath, here’s the equivalent second block with std::vector:
011836B0 mov ecx,dword ptr [esi+4]
011836B3 lea eax,[esp+28h]
011836B7 cmp eax,ecx
011836B9 jae CompleteBoxPruning+316h (01183736h)
011836BB mov edi,dword ptr [esi]
011836BD cmp edi,eax
011836BF ja CompleteBoxPruning+316h (01183736h)
011836C1 mov edx,dword ptr [esi+8]
011836C4 sub eax,edi
011836C6 sar eax,2
011836C9 mov dword ptr [esp+40h],eax
011836CD cmp ecx,edx
011836CF jne CompleteBoxPruning+302h (01183722h)
011836D1 mov eax,edx
011836D3 sub eax,ecx
011836D5 sar eax,2
011836D8 cmp eax,1
011836DB jae CompleteBoxPruning+302h (01183722h)
011836DD sub ecx,edi
011836DF sar ecx,2
011836E2 mov eax,3FFFFFFFh
011836E7 sub eax,ecx
011836E9 cmp eax,1
011836EC jb CompleteBoxPruning+4F9h (01183919h)
011836F2 inc ecx
011836F3 sub edx,edi
011836F5 sar edx,2
011836F8 mov dword ptr [esp+3Ch],ecx
011836FC mov ecx,edx
011836FE shr ecx,1
01183700 mov eax,3FFFFFFFh
01183705 sub eax,ecx
01183707 cmp eax,edx
01183709 jae CompleteBoxPruning+2EFh (0118370Fh)
0118370B xor edx,edx
0118370D jmp CompleteBoxPruning+2F1h (01183711h)
0118370F add edx,ecx
01183711 cmp edx,dword ptr [esp+3Ch]
01183715 mov ecx,esi
01183717 cmovb edx,dword ptr [esp+3Ch]
0118371C push edx
0118371D call std::vector<unsigned int,std::allocator<unsigned int> >::_Reallocate (011828F0h)
01183722 mov edx,dword ptr [esi+4]
01183725 test edx,edx
01183727 je CompleteBoxPruning+37Dh (0118379Dh)
01183729 mov eax,dword ptr [esi]
0118372B mov ecx,dword ptr [esp+40h]
0118372F mov eax,dword ptr [eax+ecx*4]
01183732 mov dword ptr [edx],eax
01183734 jmp CompleteBoxPruning+37Dh (0118379Dh)
01183736 mov edx,dword ptr [esi+8]
01183739 cmp ecx,edx
0118373B jne CompleteBoxPruning+370h (01183790h)
0118373D mov eax,edx
0118373F sub eax,ecx
01183741 sar eax,2
01183744 cmp eax,1
01183747 jae CompleteBoxPruning+370h (01183790h)
01183749 mov edi,dword ptr [esi]
0118374B sub ecx,edi
0118374D sar ecx,2
01183750 mov eax,3FFFFFFFh
01183755 sub eax,ecx
01183757 cmp eax,1
0118375A jb CompleteBoxPruning+4F9h (01183919h)
01183760 inc ecx
01183761 sub edx,edi
01183763 sar edx,2
01183766 mov dword ptr [esp+40h],ecx
0118376A mov ecx,edx
0118376C shr ecx,1
0118376E mov eax,3FFFFFFFh
01183773 sub eax,ecx
01183775 cmp eax,edx
01183777 jae CompleteBoxPruning+35Dh (0118377Dh)
01183779 xor edx,edx
0118377B jmp CompleteBoxPruning+35Fh (0118377Fh)
0118377D add edx,ecx
0118377F cmp edx,dword ptr [esp+40h]
01183783 mov ecx,esi
01183785 cmovb edx,dword ptr [esp+40h]
0118378A push edx
0118378B call std::vector<unsigned int,std::allocator<unsigned int> >::_Reallocate (011828F0h)
01183790 mov eax,dword ptr [esi+4]
01183793 test eax,eax
01183795 je CompleteBoxPruning+37Dh (0118379Dh)
01183797 mov ecx,dword ptr [esp+44h]
0118379B mov dword ptr [eax],ecx
0118379D add dword ptr [esi+4],4
011837A1 mov ecx,dword ptr [esi+4]
011837A4 mov eax,dword ptr [esp+14h]
011837A8 cmp eax,ecx
011837AA jae CompleteBoxPruning+405h (01183825h)
011837AC mov edi,dword ptr [esi]
011837AE cmp edi,eax
011837B0 ja CompleteBoxPruning+405h (01183825h)
011837B2 mov edx,dword ptr [esi+8]
011837B5 sub eax,edi
011837B7 sar eax,2
011837BA mov dword ptr [esp+3Ch],eax
011837BE cmp ecx,edx
011837C0 jne CompleteBoxPruning+3F3h (01183813h)
011837C2 mov eax,edx
011837C4 sub eax,ecx
011837C6 sar eax,2
011837C9 cmp eax,1
011837CC jae CompleteBoxPruning+3F3h (01183813h)
011837CE sub ecx,edi
011837D0 sar ecx,2
011837D3 mov eax,3FFFFFFFh
011837D8 sub eax,ecx
011837DA cmp eax,1
011837DD jb CompleteBoxPruning+4F9h (01183919h)
011837E3 inc ecx
011837E4 sub edx,edi
011837E6 sar edx,2
011837E9 mov dword ptr [esp+40h],ecx
011837ED mov ecx,edx
011837EF shr ecx,1
011837F1 mov eax,3FFFFFFFh
011837F6 sub eax,ecx
011837F8 cmp eax,edx
011837FA jae CompleteBoxPruning+3E0h (01183800h)
011837FC xor edx,edx
011837FE jmp CompleteBoxPruning+3E2h (01183802h)
01183800 add edx,ecx
01183802 cmp edx,dword ptr [esp+40h]
01183806 mov ecx,esi
01183808 cmovb edx,dword ptr [esp+40h]
0118380D push edx
0118380E call std::vector<unsigned int,std::allocator<unsigned int> >::_Reallocate (011828F0h)
01183813 mov ecx,dword ptr [esi+4]
01183816 test ecx,ecx
01183818 je CompleteBoxPruning+46Eh (0118388Eh)
0118381A mov eax,dword ptr [esi]
0118381C mov edx,dword ptr [esp+3Ch]
01183820 mov eax,dword ptr [eax+edx*4]
01183823 jmp CompleteBoxPruning+46Ch (0118388Ch)
01183825 mov edx,dword ptr [esi+8]
01183828 cmp ecx,edx
0118382A jne CompleteBoxPruning+463h (01183883h)
0118382C mov eax,edx
0118382E sub eax,ecx
01183830 sar eax,2
01183833 cmp eax,1
01183836 jae CompleteBoxPruning+45Fh (0118387Fh)
01183838 mov edi,dword ptr [esi]
0118383A sub ecx,edi
0118383C sar ecx,2
0118383F mov eax,3FFFFFFFh
01183844 sub eax,ecx
01183846 cmp eax,1
01183849 jb CompleteBoxPruning+4F9h (01183919h)
0118384F inc ecx
01183850 sub edx,edi
01183852 sar edx,2
01183855 mov dword ptr [esp+40h],ecx
01183859 mov ecx,edx
0118385B shr ecx,1
0118385D mov eax,3FFFFFFFh
01183862 sub eax,ecx
01183864 cmp eax,edx
01183866 jae CompleteBoxPruning+44Ch (0118386Ch)
01183868 xor edx,edx
0118386A jmp CompleteBoxPruning+44Eh (0118386Eh)
0118386C add edx,ecx
0118386E cmp edx,dword ptr [esp+40h]
01183872 mov ecx,esi
01183874 cmovb edx,dword ptr [esp+40h]
01183879 push edx
0118387A call std::vector<unsigned int,std::allocator<unsigned int> >::_Reallocate (011828F0h)
0118387F mov eax,dword ptr [esp+14h]
01183883 mov ecx,dword ptr [esi+4]
01183886 test ecx,ecx
01183888 je CompleteBoxPruning+46Eh (0118388Eh)
0118388A mov eax,dword ptr [eax]
0118388C mov dword ptr [ecx],eax
0118388E mov edx,dword ptr [esp+2Ch]
01183892 mov ecx,dword ptr [esp+14h]
01183896 add dword ptr [esi+4],4
That’s 180 lines of code. Instead of 27. It’s just ridiculous.
That’s all I have to say about std::vector.
———————
Now that this interlude is over, let’s go back to the sane version presented before.
The most commonly executed codepath (when an overlap is not found) has 13 instructions (it corresponds to the first block + the last block). And for 13 instructions we raised 6 potential issues. That’s a lot of questions for such a small piece of code.
Of course, we might be missing something. The compiler might know more than us. Our analysis might be too naive.
Perhaps.
Perhaps not.
How do you answer that?
As before: the scientific way. We observed. Now we need to come up with theories and tests to discern between facts and fiction.
———————
Theory: the compiler is not recent enough. A more recent compiler would produce better code.
Yeah. I heard that one before…. for every version of Visual Studio since VC6… But fair enough, it’s easy to test. In fact let’s try both VC10 (the SSE code generation has changed quite a bit between VC10 and VC11), and then VC14. VC10 gives:
00BE30FA movaps xmm1,xmmword ptr [ebx]
00BE30FD movaps xmm2,xmmword ptr [esp+40h]
00BE3102 cmpltps xmm2,xmm1
00BE3106 movmskps eax,xmm2
00BE3109 cmp eax,0Ch
00BE310C jne CompleteBoxPruning+3FEh (0BE315Eh)
00BE310E mov ecx,dword ptr [esi+4]
00BE3111 cmp ecx,dword ptr [esi]
00BE3113 jne CompleteBoxPruning+3BEh (0BE311Eh)
00BE3115 push 1
00BE3117 mov ecx,esi
00BE3119 call IceCore::Container::Resize (0BE1240h)
00BE311E mov edx,dword ptr [esi+4]
00BE3121 mov eax,dword ptr [esi+8]
00BE3124 mov ecx,dword ptr [esp+30h]
00BE3128 mov dword ptr [eax+edx*4],ecx
00BE312B inc dword ptr [esi+4]
00BE312E mov eax,dword ptr [esi+4]
00BE3131 mov edx,dword ptr [edi]
00BE3133 mov dword ptr [esp+34h],edx
00BE3137 cmp eax,dword ptr [esi]
00BE3139 jne CompleteBoxPruning+3E4h (0BE3144h)
00BE313B push 1
00BE313D mov ecx,esi
00BE313F call IceCore::Container::Resize (0BE1240h)
00BE3144 mov eax,dword ptr [esi+4]
00BE3147 mov ecx,dword ptr [esi+8]
00BE314A mov edx,dword ptr [esp+34h]
00BE314E movss xmm0,dword ptr [esp+38h]
00BE3154 mov dword ptr [ecx+eax*4],edx
00BE3157 inc dword ptr [esi+4]
00BE315A mov ecx,dword ptr [esp+3Ch]
00BE315E mov eax,dword ptr [esp+28h]
00BE3162 add eax,8
00BE3165 add ebx,10h
00BE3168 add edi,4
00BE316B comiss xmm0,dword ptr [eax]
00BE316E mov dword ptr [esp+28h],eax
00BE3172 jae CompleteBoxPruning+39Ah (0BE30FAh)
There are still 13 instructions overall in the main codepath, with a few twists.
It seems to use three xmm registers instead of two, which looks better.
———————
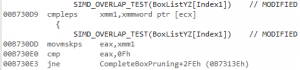
This is the same as in VC11, but using two instructions instead of one:
00BE30FA movaps xmm1,xmmword ptr [ebx]
…
00BE3102 cmpltps xmm2,xmm1
xmm2 is still destroyed all the time, and reloaded from the stack:
00BE30FD movaps xmm2,xmmword ptr [esp+40h]
The only difference is that it’s reloaded in our first block, rather than in the third block before. But it’s really all the same otherwise - even the stack offset is the same.
Questions 1 and 2: same.
———————
VC10 seems to manage “MaxLimit” better. It’s kept in xmm0 and only reloaded when an overlap occurs:
00BE314E movss xmm0,dword ptr [esp+38h]
Well done.
Question 3: VC10 wins.
———————
In the third block, what used to be ecx is now eax:
00BE3162 add eax,8
…
00BE316B comiss xmm0,dword ptr [eax]
00BE316E mov dword ptr [esp+28h],eax
And it’s saved to the stack all the time, like in VC11.
As for edi (previously edx), it is not saved to the stack anymore. Yay!
But eax (previously ecx) is now reloaded from the stack all the time:
00BE315E mov eax,dword ptr [esp+28h]
…while it wasn’t before. Oh.
Question 4: VC11 wins.
Question 5 and 6: the same overall.
———————
So from just looking at this short snippet it is unclear which compiler does a better job. But then if you look at the code before that inner loop, you find this:
0BE2F1B fstp dword ptr [eax-58h]
00BE2F1E fld dword ptr [edx+8]
00BE2F21 fstp dword ptr [eax-54h]
00BE2F24 fld dword ptr [edx+10h]
00BE2F27 fstp dword ptr [eax-50h]
00BE2F2A fld dword ptr [edx+14h]
00BE2F2D fstp dword ptr [eax-4Ch]
00BE2F30 mov edx,dword ptr [esi-14h]
00BE2F33 mov dword ptr [edi-14h],edx
00BE2F36 lea edx,[edx+edx*2]
00BE2F39 fld dword ptr [ebx+edx*8]
00BE2F3C lea edx,[ebx+edx*8]
00BE2F3F fstp dword ptr [ecx-2Ch]
00BE2F42 fld dword ptr [edx+0Ch]
00BE2F45 fstp dword ptr [ecx-28h]
00BE2F48 fld dword ptr [edx+4]
00BE2F4B fstp dword ptr [eax-48h]
00BE2F4E fld dword ptr [edx+8]
00BE2F51 fstp dword ptr [eax-44h]
00BE2F54 fld dword ptr [edx+10h]
00BE2F57 fstp dword ptr [eax-40h]
00BE2F5A fld dword ptr [edx+14h]
00BE2F5D fstp dword ptr [eax-3Ch]
00BE2F60 mov edx,dword ptr [esi-10h]
00BE2F63 mov dword ptr [edi-10h],edx
00BE2F66 lea edx,[edx+edx*2]
00BE2F69 fld dword ptr [ebx+edx*8]
00BE2F6C lea edx,[ebx+edx*8]
00BE2F6F fstp dword ptr [ecx-24h]
00BE2F72 fld dword ptr [edx+0Ch]
00BE2F75 fstp dword ptr [ecx-20h]
00BE2F78 fld dword ptr [edx+4]
00BE2F7B fstp dword ptr [eax-38h]
00BE2F7E fld dword ptr [edx+8]
00BE2F81 fstp dword ptr [eax-34h]
00BE2F84 fld dword ptr [edx+10h]
00BE2F87 fstp dword ptr [eax-30h]
00BE2F8A fld dword ptr [edx+14h]
00BE2F8D fstp dword ptr [eax-2Ch]
00BE2F90 mov edx,dword ptr [esi-0Ch]
00BE2F93 mov dword ptr [edi-0Ch],edx
00BE2F96 lea edx,[edx+edx*2]
00BE2F99 fld dword ptr [ebx+edx*8]
00BE2F9C lea edx,[ebx+edx*8]
00BE2F9F fstp dword ptr [ecx-1Ch]
00BE2FA2 fld dword ptr [edx+0Ch]
00BE2FA5 fstp dword ptr [ecx-18h]
00BE2FA8 fld dword ptr [edx+4]
00BE2FAB fstp dword ptr [eax-28h]
00BE2FAE fld dword ptr [edx+8]
00BE2FB1 fstp dword ptr [eax-24h]
00BE2FB4 fld dword ptr [edx+10h]
00BE2FB7 fstp dword ptr [eax-20h]
00BE2FBA fld dword ptr [edx+14h]
00BE2FBD fstp dword ptr [eax-1Ch]
Yikes!!
Ok: VC10 still used x87 instructions here and there. VC11 did not.
Forget that inner loop analysis: advantage VC11, big time. The benchmark results confirm this, regardless of the instructions count:
Office PC / unsafe version:
Complete test (brute force): found 11811 intersections in 891760 K-cycles.
19379 K-cycles.
18483 K-cycles.
18943 K-cycles.
18093 K-cycles.
18321 K-cycles.
18417 K-cycles.
18078 K-cycles.
19035 K-cycles.
18500 K-cycles.
18092 K-cycles.
18329 K-cycles.
18092 K-cycles.
17899 K-cycles.
18524 K-cycles.
18085 K-cycles.
19308 K-cycles.
Complete test (box pruning): found 11715 intersections in 17899 K-cycles.
=> Much slower than what we got with VC11.
———————
So, VC14 then? Let’s have a look:
00F32F33 cmpltps xmm1,xmmword ptr [edi]
00F32F37 movmskps eax,xmm1
00F32F3A cmp eax,0Ch
00F32F3D jne CompleteBoxPruning+2D1h (0F32F91h)
00F32F3F mov eax,dword ptr [esi+4]
00F32F42 cmp eax,dword ptr [esi]
00F32F44 jne CompleteBoxPruning+28Fh (0F32F4Fh)
00F32F46 push 1
00F32F48 mov ecx,esi
00F32F4A call IceCore::Container::Resize (0F312D0h)
00F32F4F mov ecx,dword ptr [esi+4]
00F32F52 mov eax,dword ptr [esi+8]
00F32F55 mov edx,dword ptr [esp+34h]
00F32F59 mov dword ptr [eax+ecx*4],edx
00F32F5C mov edx,dword ptr [esp+20h]
00F32F60 inc dword ptr [esi+4]
00F32F63 mov eax,dword ptr [esi+4]
00F32F66 mov ecx,dword ptr [edx]
00F32F68 mov dword ptr [esp+30h],ecx
00F32F6C cmp eax,dword ptr [esi]
00F32F6E jne CompleteBoxPruning+2B9h (0F32F79h)
00F32F70 push 1
00F32F72 mov ecx,esi
00F32F74 call IceCore::Container::Resize (0F312D0h)
00F32F79 mov ecx,dword ptr [esi+4]
00F32F7C mov eax,dword ptr [esi+8]
00F32F7F mov edx,dword ptr [esp+30h]
00F32F83 mov dword ptr [eax+ecx*4],edx
00F32F86 inc dword ptr [esi+4]
00F32F89 mov ecx,dword ptr [esp+28h]
00F32F8D mov edx,dword ptr [esp+20h]
00F32F91 movss xmm0,dword ptr [esp+38h]
00F32F97 add ecx,8
00F32F9A movaps xmm1,xmmword ptr [esp+40h]
00F32F9F add edx,4
00F32FA2 add edi,10h
00F32FA5 mov dword ptr [esp+20h],edx
00F32FA9 mov dword ptr [esp+28h],ecx
00F32FAD comiss xmm0,dword ptr [ecx]
00F32FB0 jae CompleteBoxPruning+273h (0F32F33h)
This one will be quick: some instructions have been re-ordered in the third block, but other than that it’s exactly the same code as VC11’s. And pretty much exactly the same performance.
So, nope, a newer compiler doesn’t solve the issues.
But are they really issues? There’s more to performance than the instructions count, as we saw before. Are we chasing a red herring?
To find our answers, we must go closer to the metal. And that’s what we will do next time.
———————
What we learnt:
Different compilers will give different results.
Compilers are getting better all the time, but they’re still not perfect.
std::vector sucks.