Coder Corner

Part 3: don’t trust the compiler

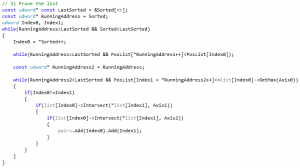
We now look at the “CompleteBoxPruning” function for the first time. This is my code but since I wrote it 15 years ago, it’s pretty much the same for me as it is for you: I am looking at some foreign code I do not recognize much.

I suppose the first thing to do is to analyze it and get a feeling for what takes time. There is an allocation:

Then a loop to fill that buffer:

Then we sort this array:

And then the rest of the code is the main pruning loop that scans the array and does overlap tests:

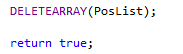
After that we just free the array we allocated, and return:

Ok, so, we can forget the allocation: allocations are bad and should be avoided if possible, but on PC, in single-threaded code like this, one allocation is unlikely to be an issue - unless not much else is happening. That leaves us with basically two parts: the sorting, and the pruning. I suppose this makes total sense for an algorithm usually called either “sweep-and-prune” or “sort-and-sweep” – the “box pruning” term being again just how I call this specific variation on the theme: single sorting axis, direct results, no persistent data.

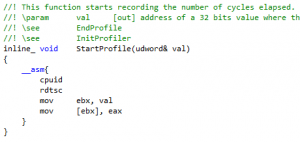
So first, let’s figure out how much time we spend in the sorting, and how much time in the pruning. We could use a profiler, or add extra rdtsc calls in there. Let’s try the rdtsc stuff. That would be an opportunity for me to tell you that the code in its current form will not compile for x64, because inline assembly is forbidden there. So the profiler functions for example do not compile:

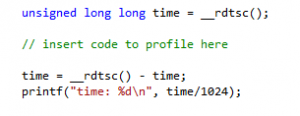
This is easy to fix though: these days there is a __rdtsc() intrinsic that you can use instead, after including <intrin.h>. Let’s try that here. You can include the header and write something like this around the code you want to measure:

If we apply this to the different sections of the code, we get the following results:

Allocation:
time: 3
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1
time: 1

Remember that we looped several times over the “CompleteBoxPruning” function to get more stable results. Typically what happens then is that the first call is significantly more expensive than the other ones, because everything gets pulled in the cache (i.e. you get a lot more cache misses than usual). When optimizing a function, you need to decide if you want to optimize for the “best case”, the “average case”, or the “worst case”.

The best case is when everything is nicely in the cache, you don’t get much cache misses, and you can focus on things like decreasing the total number of instructions, using faster instructions, removing branches, using SIMD, etc.

The worst case is the first frame, when cache misses are unavoidable. To optimize this, you need to reduce the number of cache misses, i.e. decrease the size of your structures, use more cache-friendly access patterns, use prefetch calls judiciously, etc.

The average case is a fuzzy mix of both: in the real world you get a mixture of best & worst cases depending on what the app is doing, how often the function is called, etc, and at the end of the day, on average, everything matters. There is no right answer here, no hierarchy: although it is good practice to “optimize the worst case”, all of it can be equally important.

At this point the main thing is to be aware of these differences, and to know approximately if the optimization you’re working on will have an impact on the worst case or not. It is relatively common to work on a “best case” optimization that seems wonderful “in the lab”, in an isolated test app, and then realize that it doesn’t make any actual difference once put “in the field” (e.g. in a game), because the cost becomes dominated by cache misses there.

For now we are in the lab, so we will just be aware of these things, notice that the first frame is more expensive, and ignore it. If you think about it too much, you never even get started.

Sorting (static):
time: 686
time: 144
time: 139
time: 145
time: 138
time: 138
time: 138
time: 148
time: 139
time: 137
time: 138
time: 138
time: 137
time: 138
time: 146
time: 144

The sorting is at least 140 times more expensive than the allocation in our test. Thus, as expected, we’re just going to ignore the allocation for now. That was only a hunch before, but profiling confirms it was correct.

The first frame is almost 5 times more expensive than the subsequent frames, which seems a bit excessive. This comment explains why:

The code is using my old radix sort, which has a special trick to take advantage of temporal coherence. That is, if you keep sorting the same objects from one frame to the next, sometimes the resulting order will be the same. Think for example about particles being sorted along the view axis: their order is going to be roughly the same from one frame to the next, and that’s why e.g. a bubble-sort can work well in this case - it terminates early because there is not much work needed (or no work at all indeed) to get from the current ordering to the new ordering. The radix sort uses a similar idea: it starts sorting the input data using the sorted ranks from the previous call, then notices that the ranks are still valid (the order hasn’t changed), and immediately returns. So it actually skips all the radix passes. That’s why the first frame is so much more expensive: it’s the only frame actually doing the sorting!

To see the actual cost of sorting, we can remove the static keyword. That gives:

Sorting (non static):
time: 880
time: 467
time: 468
time: 471
time: 471
time: 470
time: 469
time: 469
time: 499
time: 471
time: 471
time: 490
time: 470
time: 471
time: 470
time: 469

That’s more like it. The first frame becomes more expensive for some reason (maybe because we now run the ctor/dtor inside that function, i.e. we allocate/deallocate memory), and then the subsequent frames reveal the real cost of radix-sorting the array. The first frame is now less than 2X slower, i.e. the cost of cache misses is not as high as we thought.

In any case, this is all irrelevant for now, because:

Pruning:
time: 93164
time: 94527
time: 95655
time: 93348
time: 94079
time: 93220
time: 93076
time: 94709
time: 93059
time: 92900
time: 93033
time: 94699
time: 94626
time: 94186
time: 92811
time: 95747

There it is. That’s what takes all the time. The noise (the variation) in the timings is already more expensive than the full non-static radix sorting. So we will just put back the static sorter and ignore it entirely for now. In this test, questions like “is radix sort the best choice here?” or “shouldn’t you use quick-sort instead?” are entirely irrelevant. At least for now, with that many boxes, and in this configuration (the conclusion might be different with less boxes, or with boxes that do not overlap each-other that much, etc), the sorting costs nothing compared to the pruning.

And then we can look at the last part:

Deallocation:
time: 4
time: 3
time: 3
time: 3
time: 6
time: 3
time: 3
time: 3
time: 3
time: 3
time: 3
time: 3
time: 3
time: 3
time: 3
time: 3

Nothing to see here, it is interesting to note that the deallocation is more expensive than the allocation, but this is virtually free anyway.

So, analysis is done: we need to attack the pruning loop, everything else can wait.

Let’s look at the loop again:

There isn’t much code but since we have a lot of objects (10000), any little gain from any tiny optimization will also be multiplied by 10000 - and become measurable, if not significant.

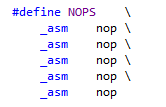
If you look at the C++ code and you have no idea, you can often switch to the disassembly in search of inspiration. To make it more readable, I often use a NOP macro like this one:

And then I wrap the code I want to inspect between nops, like this for example:

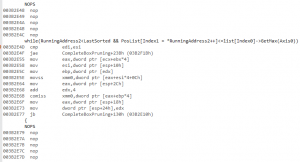
It allows me to isolate the code in the assembly, which makes it a lot easier to read:

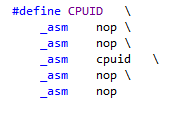
Note that the nops don’t prevent the compiler from reorganizing the instructions anyway, and sometimes an instruction you want to monitor can still move outside of the wrapped snippet. In this case you can use the alternative CPUID macro which puts a serializing cpuid instruction in the middle of the nops:

It puts more restrictions on generated code and makes it easier to analyze, but it also makes things very slow - in our case here it makes the optimized loop slower than the brute-force loop. It also sometimes changes the code too much compared to what it would be “for real”, so I usually just stick with nops, unless something looks a bit fishy and I want to double-check what is really happening.

Now, let’s look at the disassembly we got there.

While decorating the code with nops does not make everything magically obvious, there are still parts that are pretty clear right from the start: the cmp/jae is the first comparison (”while(RunningAddress2<LastSorted”) and the comiss/jb is the second one (”&& PosList[Index1 = *RunningAddress2++]<=list[Index0]->GetMax(Axis0))”).

Now the weird bit is that we first read something from memory and put it in xmm0 (”movss xmm0,dword ptr [eax+esi*4+0Ch]“), and then we compare this to some other value we read from memory (”comiss xmm0,dword ptr [eax+ebp*4]“). But in the C++ code, “list[Index0]->GetMax(Axis0)” is actually a constant for the whole loop. So why do we read it over and over from memory? It seems to me that the first movss is doing the “list[Index0]->GetMax(Axis0)”. It’s kind of obvious from the 0Ch offset in the indexing: we’re reading a “Max” value from the bounds, they start at offset 12 (since the mins are located first and they’re 4 bytes each), so that 0Ch must be related to it. And thus, it looks like the compiler decided to read that stuff from memory all the time instead of keeping it in a register.

Why? It might have something to do with aliasing. The pointers are not marked as restricted so maybe the compiler detected that there was a possibility for “list” to be modified within the loop, and thus for that limit value to change from one loop iteration to the next. Or maybe it is because “Index0″ and “Axis0″ are not const.

Or something else.

I briefly tried to use restricted pointers, to add const, to help the compiler see the light.

I failed.

At the end of the day, the same old advice remained: don’t trust the compiler. Never ever assume that it’s going to “see” the obvious. And even if yours does, there is no guarantee that another compiler on another platform will be as smart.

To be fair with compilers, they may actually be too smart. They might see something we don’t. They might see a perfectly valid (yet obscure and arcane) reason that prevents them from doing the optimization themselves.

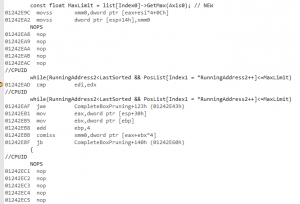
In any case whatever the reason we reach the same conclusion: don’t rely on the compiler. Don’t assume the compiler will do it for you. Do it yourself. Write it this way:

And suddenly the disassembly makes sense:

The load with the +0Ch is now done before the loop, and the code between the nops became smaller. It is not perfect still: do you see the line that writes xmm0 to the stack ? (”movss dword ptr [esp+14h],xmm0″). You find it again a bit later like this:

So the compiler avoids the per-loop computation of MaxLimit (yay!) but instead of keeping it in one of the unused XMM registers (there are plenty: the code only uses one at this point), it writes it once to the stack and then reloads it from there, all the time (booh!).

Still, that’s enough for now. By moving the constant “MinLimit” and “MaxLimit” values out of the loops, in explicit const float local variables, we get the following timings:

Office PC:

Complete test (brute force): found 11811 intersections in 819967 K-cycles.
89037 K-cycles.
98463 K-cycles.
95177 K-cycles.
88952 K-cycles.
89091 K-cycles.
88540 K-cycles.
89151 K-cycles.
91734 K-cycles.
88352 K-cycles.
88395 K-cycles.
99091 K-cycles.
99361 K-cycles.
91971 K-cycles.
89706 K-cycles.
88949 K-cycles.
89276 K-cycles.
Complete test (box pruning): found 11811 intersections in 88352 K-cycles.

Home PC:

Complete test (brute force): found 11811 intersections in 781863 K-cycles.
96888 K-cycles.
93316 K-cycles.
93168 K-cycles.
93235 K-cycles.
93242 K-cycles.
93720 K-cycles.
93199 K-cycles.
93725 K-cycles.
93145 K-cycles.
93488 K-cycles.
93390 K-cycles.
93346 K-cycles.
93138 K-cycles.
93404 K-cycles.
93268 K-cycles.
93335 K-cycles.
Complete test (box pruning): found 11811 intersections in 93138 K-cycles.

The gains are summarized here:

“Delta” and “Speedup” are computed between current version and previous version. “Overall X factor” is computed between current version and the base version (version 2).

The base version is version2 to be fair, since version1 was the same code, just not using the proper compiler settings.

The code became faster. On the other hand the total number of instructions increased to 198. This is slightly irrelevant though: some dummy instructions are sometimes added just to align loops on 16-byte boundaries, reducing the number of instructions does not always make things faster, all instructions do not have the same cost (so multiple cheap instructions can be faster than one costly instruction), etc. It is however a good idea to keep an eye on the disassembly, and the number of instructions used in the inner loop still gives a hint about the current state of things, how much potential gains there are out there, whether an optimization had any effect on the generated code, and so on.

What we learnt:

Don’t trust the compiler.

Don’t assume it’s going to do it for you. Do it yourself if you can.

Always check the disassembly.

That’s enough for one post.

Next time we will stay focused on these ‘while’ lines and optimize them further.

GitHub code for part 3

Part 2 - compiler options

After converting the project, the default compiler options for the Release configuration are as follows (click to expand):

These are basically the only options affecting performance, if we ignore a few additional ones in the linker. After some years programming, you get a feeling for which ones of these options are important, and which ones are not.

So… what do you think, optimization experts?
Which one of these will make the most difference here?

For me, looking at that list, the suspicious ones that should be changed immediately are the following:

Inline Function Expansion: Default

Enable C++ Exceptions: Yes (/EHsc)

Enable Enhanced Instruction Set: Not Set

Floating Point Model: Precise (/fp:precise)

These guys are the usual suspects, as far as I’m concerned.

But let’s test this.

—

We first change the “Inline Function Expansion” option from “Default” to “Only __inline (/Ob1)”

Results:

Complete test (brute force): found 11811 intersections in 837222 K-cycles.

Complete test (box pruning): found 11811 intersections in 96230 K-cycles.

In general, inlining has a strong impact on performance, and there would be a need for an entirely separate blog post about the art of inlining. But in this specific case, it does not make any difference: the “Default” setting works well enough. The disassembly is the same 202 instructions as before so it did not change anything.

Note that it does not mean nothing gets inlined. “Default” does not mean “no inlining“. If you really disable inlining with the “Disabled /Ob0” option, you get the following results:

Complete test (brute force): found 11811 intersections in 1155114 K-cycles.

Complete test (box pruning): found 11811 intersections in 174538 K-cycles.

That is quite a difference. So clearly, inlining is one of the important things to get right, and in this specific case the default option is already right.

Good.

Now, we switch inlining back to “Default” and move on to the next option.

—–

This time we disable exceptions (“Enable C++ Exceptions: No”).

Results:

Complete test (brute force): found 11811 intersections in 817837 K-cycles.

Complete test (box pruning): found 11811 intersections in 95789 K-cycles.

It appears that disabling exceptions has a noticeable effect on the brute-force implementation, but no clear effect on the box-pruning function.

The disassembly shows the same 202 instructions as before, so the small performance gain is not actually here, it’s just noise in the results. It is important to check the disassembly to confirm that the “optimization” actually changed something. Otherwise you can often see what you want to see in the results…

Well, exceptions usually add a tiny overhead for each function, and it can accumulate and add up to “a lot” (relatively speaking). But we don’t have a lot of functions here, and as we just saw before with inlining, the few functions we have are properly inlined. So it makes sense that disabling exceptions in this case does not change much.

Worth checking though. Don’t assume. Check and check and check.

—–

Next, we turn exceptions back on (to measure the effect of each option individually) and then we move on to this:

Enable Enhanced Instruction Set: Not Set

This one is interesting. The default is “Not Set” but if you look at the disassembly so far, it is clearly using some SSE registers (for example xmm0). So it turns out that by default, the compiler uses SSE instructions these days. Which explains why switching to /arch:SSE2 gives these results:

Complete test (brute force): found 11811 intersections in 829134 K-cycles.

Complete test (box pruning): found 11811 intersections in 96448 K-cycles.

Again it appears that the option has a small effect on the brute-force code (if this isn’t just noise), and no effect on the box-pruning code. And indeed, the disassembly shows the same 202 instructions as before.

Now, as an experiment, we can switch back to regular x87 code with the /arch:IA32 compiler flag (”Enable Enhanced Instruction Set : No Enhanced Instructions”). This gives the following results:

Complete test (brute force): found 11811 intersections in 921893 K-cycles.

Complete test (box pruning): found 11811 intersections in 110605 K-cycles.

Ok, so that makes more sense: using SSE2 does in fact have a clear impact on performance, it’s just that the default “Not Set” option was actually already using it. That’s a bit confusing, but at least the results now make sense.

While we are looking at these results, please note how enabling the SSE2 compiler flag only provides modest gains, from ~110000 to ~97000: that’s about a 10% speedup only. This is again why we didn’t enable that compile flag back in PhysX 2.x. Contrary to what naive users claimed online, using the flag does not magically make your code 4X faster.

—–

Finally, we focus our attention on the Floating Point Model, and switch it to /fp:fast. You might guess the results by now:

Complete test (brute force): found 11811 intersections in 825688 K-cycles.

Complete test (box pruning): found 11811 intersections in 96115 K-cycles.

And yes, the disassembly is exactly the same as before. Frustrating.

—–

At that point I got tired of what looked like a pointless experiment. I just quickly setup the remaining options with my usual settings, compiled, and…

…the code got measurably faster:

Complete test (brute force): found 11811 intersections in 817855 K-cycles.

Complete test (box pruning): found 11811 intersections in 93208 K-cycles.

Like, a 100% reproducible good 3000 K-Cycles faster.

And the speedup was not imaginary, it was indeed reflected in the disassembly: 192 instructions.

What…

After a short investigation I discovered that the only compiler option that made any difference, the one responsible for the speedup was “Omit Frame Pointers“.

…the hell?

So, experts, did you predict that?

I did not.

This was doubly surprising to me.

The first surprise is that /O2 (which was enabled by default in Release, right from the start) is supposed to include /Oy, i.e. the “Omit Frame Pointers” optimization.

But this link explains the problem:

“The /Ox (Full Optimization) and /O1, /O2 (Minimize Size, Maximize Speed) options imply /Oy. Specifying /Oy– after the /Ox, /O1, or /O2 option disables /Oy, whether it is explicit or implied.”

So, the issue is that the combo box in the compiler options exposes “No (/Oy-)”, which is an explicit “disable” command rather than a “use whatever is the default”. So as the MSDN says, it overrides and undoes the /O2 directive. Oops.

The second surprise for me was that it had such a measurable impact on performance: about 5%. Not bad for something that wasn’t even on my radar. To be fair this issue doesn’t exist with 64-bit builds (as far as I know), so maybe that’s why I never saw that one before. According to the MSDN /Oy frees up one more register, EBP, for storing frequently used variables and sub-expressions. Somehow I didn’t realize that before, and it certainly explains why things get faster.

—–

Ok!

Compiler options: checked!

Other than that, I removed some obsolete files from the project, but made no code changes. This version is now going to be our base version against which the next optimizations will be measured.

For reference, this was my best run on the office PC:

Complete test (brute force): found 11811 intersections in 819814 K-cycles.
102256 K-cycles.
93092 K-cycles.
92885 K-cycles.
99537 K-cycles.
93146 K-cycles.
93325 K-cycles.
95795 K-cycles.
97573 K-cycles.
97606 K-cycles.
98829 K-cycles.
97040 K-cycles.
95197 K-cycles.
98149 K-cycles.
93226 K-cycles.
93008 K-cycles.
95254 K-cycles.
Complete test (box pruning): found 11811 intersections in 92885 K-cycles.

And on the home PC:

Complete test (brute force): found 11811 intersections in 781996 K-cycles.
102578 K-cycles.
98972 K-cycles.
98898 K-cycles.
99183 K-cycles.
98920 K-cycles.
98823 K-cycles.
98948 K-cycles.
99047 K-cycles.
99132 K-cycles.
98822 K-cycles.
98975 K-cycles.
100701 K-cycles.
98892 K-cycles.
99025 K-cycles.
99294 K-cycles.
98981 K-cycles.
Complete test (box pruning): found 11811 intersections in 98822 K-cycles.

The progress will be captured in this table:

What we learnt:

The default performance-related compiler options in Release mode are pretty good these days, but you can still do better if you go there and tweak them.

Next time, we will start looking at the code and investigate what we can modify. That is, we will start the proper optimizations.

GitHub code for part 2

Part 1 - The setup

Back in 2002 I released a small “box pruning” library on my website. Basically, this is a “broadphase” algorithm: given a set of input bounds (AABBs - for Axis Aligned Bounding Boxes), it finds the subset of overlapping bounds (reported as an array of overlapping pairs). There is also a “bipartite” version that finds overlapping boxes between two sets of input bounds. For more details about the basics of box pruning, please refer to this document.

Note that “box pruning” is not an official term. That’s just how I called it some 15 years ago.

Since then, the library has been used in a few projects, commercial or otherwise. It got benchmarked against alternative approaches: for example you could still find it back in Bullet 2.82’s “Extras\CDTestFramework” folder, tested against Bullet’s internal “dbVt” implementation. People asked questions. People sent suggestions. And up until recently, people sent me results showing how their own alternative broadphase implementation was faster than mine. The last time that happened, it was one of my coworkers, somebody sitting about a meter away from me in the office, who presented his hash-grid based broadphase which was “2 to 3 times faster” than my old box pruning code.

That’s when I knew I had to update this library. Because, of course, I’ve made that code quite a bit faster since then.

Even back in 2002, I didn’t praise that initial implementation for its performance. The comments in there mention the “sheer simplicity”, explicitly saying that it is “probably not faster” than the other competing algorithms from that time. This initial code was also not using optimizations that I wrote about later in the SAP document, e.g. the use of “sentinels” to simplify the inner loop. Thus, clearly, it was not optimal.

And then of course, again: it’s been 15 years. I learnt a few things since then. The code I write today is often significantly better and faster than the code I wrote 15 years ago. Even if my old self would have had a hard time accepting that.

So, I thought I could write a series of blog posts about how to optimize that old implementation from 2002, and make it a good deal faster. Like, I don’t know, let’s say an order of magnitude faster as a target.

Sounds good?

Ok, let’s start.

For this initial blog post I didn’t do any real changes, I am just setting up the project. The old version was compiled with VC6, which I unfortunately don’t have anymore. For this experiment I randomly picked VC11.

Here is a detailed list of what I did:

• Converted the project from Visual Studio 6 to Visual Studio 2012. I used the automatic conversion and didn’t tweak any project settings. I used whatever was enabled after the conversion. We will investigate the compiler options in the next post.
• Made it compile again. There were some missing loop indices in the radix code, because earlier versions of Visual Studio were notoriously not properly handling the scope in for loops (see /Zc::forScope). Other than that it compiled just fine.
• Moved the files that will not change in these experiments to a shared folder outside of the project. That way I can have multiple Visual Studio projects capturing various stages of the experiment without copying all these files in each of them.
• Added a new benchmark. In the old version there was a single test using the “CompleteBoxPruning” function, with a configuration that used 5000 boxes and returned 200 overlapping pairs. This is a bit too small to properly stress test the code, so I added a new test that uses 10000 boxes and returns 11811 intersections. That’s enough work to make our optimizations measurable. Otherwise they can be invisible and lost in the noise.
• In this new test (”RunPerformanceTest” function) I loop multiple times over the “BruteForceCompleteBoxTest” and “CompleteBoxPruning” tests to get more stable results (recording the ‘min’). Reported timing values are divided by 1024 to get results in “K-Cycles”.
• I also added a validity test (”RunValidityTest” function) to make sure that the two functions, brute-force and optimized, keep reporting the same pairs.

And that’s about it. There are no modifications to the code otherwise for now; it is the same code as in 2002.

The initial results are as follows, on my home PC and my office PC. The CPU-Z profiles for both machines are available here:

Home PC: pierre-pc

Office PC: pterdiman-dt

Note that they aren’t really “killer” machines. They are kind of old and not super fast. That’s by design. Optimizing things on the best & latest PC often hides issues that the rest of the world may suffer from. So you ship your code thinking it’s fast, and immediately get reports about performance problems from everybody. Not good. I do the opposite, and (try to) make the code run fast on old machines. That way there’s no bad surprises. For similar reasons I test the results on at least two machines, because sometimes one optimization only works on one, and not on the other. Ideally I could / should have used entirely different platforms here (maybe running the experiments on consoles), but I’m not sure how legal it is to publish benchmark results from a console, so, maybe next time.

Home PC:

Complete test (brute force): found 11811 intersections in 795407 K-cycles.
102583 K-cycles.
102048 K-cycles.
101721 K-cycles.
101906 K-cycles.
101881 K-cycles.
101662 K-cycles.
101768 K-cycles.
101693 K-cycles.
102094 K-cycles.
101924 K-cycles.
101696 K-cycles.
101964 K-cycles.
102000 K-cycles.
101789 K-cycles.
101982 K-cycles.
101917 K-cycles.
Complete test (box pruning): found 11811 intersections in 101662 K-cycles.

Office PC:

Complete test (brute force): found 11811 intersections in 814615 K-cycles.
106695 K-cycles.
96859 K-cycles.
97934 K-cycles.
99237 K-cycles.
97394 K-cycles.
97002 K-cycles.
96746 K-cycles.
96856 K-cycles.
98473 K-cycles.
97249 K-cycles.
96655 K-cycles.
102757 K-cycles.
96203 K-cycles.
96661 K-cycles.
107484 K-cycles.
104195 K-cycles.
Complete test (box pruning): found 11811 intersections in 96203 K-cycles.

The “brute force” version uses the unoptimized O(N^2) “BruteForceCompleteBoxTest” function, and it is mainly there to check the returned number of pairs is valid. I only report one performance number for this case - we don’t care about it.

The “box pruning” version uses the “CompleteBoxPruning” function, that we are going to optimize. As we can see here, this initial implementation offered quite decent speedups already - not bad for something that was about 50 lines of vanilla C++ code.

For the “complete box pruning case” I make the code run 16 times and record the minimum time. I am going to report the 16 numbers from the 16 runs though, to show how stable the machines are (i.e. do we get reproducible results or is it just random?), and to show the cost of the first run (which is usually more expensive than the subsequent runs, so it’s a worst-case figure).

These results are out-of-the-box after the automatic project conversion. Needless to say, this is compiled in Release mode.

If you want to replicate these numbers and get stable benchmark results from one run to the next, make sure your PC is properly setup for minimal interference. See for example the first paragraphs in this post .

For now I will only focus on the “CompleteBoxPruning” function, completely ignoring its “BipartiteBoxPruning” counterpart in my reports. All optimizations will be equally valid for the bipartite case, but there will be enough to say and report with just one function for now. The companion code might update and optimize the bipartite function along the way though - I’ll just not talk about it.

The initial disassembly for the function has 202 instructions. We are going to keep a close eye on the disassembly in this project.

That’s it for now.

Next time, we will play with the compiler options and see what kind of speedup we can get “for free”.

GitHub code for part 1