Coder Corner

Here.

Part 14d – integer comparisons redux

In this part, we complete the port of Fabian Giesen’s code (version 14b) to C++.

In part 7 we replaced float comparisons with integer comparisons (a very old trick), but dismissed the results because the gains were too small to justify the increase in code complexity. However we made the code significantly faster since then, so the relatively small gains we got at the time might be more interesting today.

Moreover, Fabian’s version uses integers for the X’s values only. This may also be a more interesting strategy than using them for everything, like in version 7.

Let’s try!

Replicating this in the C++ version is trivial. Read part 7 again for the details. The only difference is that Fabian uses a different function to encode the floats:

// Munge the float bits to return produce an unsigned order-preserving
// ranking of floating-point numbers.
// (Old trick: http://stereopsis.com/radix.html FloatFlip, with a new
// spin to get rid of -0.0f)
// In /fp:precise, we can just calc “x + 0.0f” and get what we need.
// But fast math optimizes it away. Could use #pragma float_control,
// but that prohibits inlining of MungeFloat. So do this silly thing
// instead.
float g_global_this_always_zero = 0.0f;
static inline udword MungeFloat(float f)
{
union
{
float f;
udword u;
sdword s;
} u;
u.f = f + g_global_this_always_zero; // NOT a nop! Canonicalizes -0.0f to +0.0f
udword toggle = (u.s >> 31) | (1u << 31);
return u.u ^ toggle;
}

While my version from part 7 was simply:

static __forceinline udword encodeFloat(udword ir)
{
if(ir & 0×80000000) //negative?
return ~ir;//reverse sequence of negative numbers
else
return ir | 0×80000000; // flip sign
}

So it’s pretty much the same: given the same input float, the two functions return the same integer value, except for -0.0f. But that’s because Fabian’s code transforms -0.0f to +0.0f before doing the conversion to integer, it’s not a side-effect of the conversion itself.

This is not really needed, since both the sorting code and the pruning code can deal with -0.0f just fine. However it is technically more correct, i.e. more in line with what float comparisons would give, since with floats a positive zero is equal to a negative zero. So it is technically more correct to map both to the same integer value – which is what Fabian’s code does.

In practice, it means that my version could produce “incorrect” results when positive and negative zeros are involved in the box coordinates. But it would only happen in edge cases where boxes exactly touch, so it would be as “incorrect” as our “unsafe” versions from past posts, and we already explained why they weren’t a big issue. Still, Fabian’s version is technically superior, even if the code does look a bit silly indeed - but in a cute kind of way.

Now a perhaps more interesting thing to note is that Fabian’s version (well, Michael Herf’s version I suppose) is branchless. So could it be measurably faster?

Without further ado, here are the results on my machines – new entries in bold letters:

Version 14d uses integer comparisons for X’s. The P variant uses Pierre’s encoding function (“encodeFloat”), while the F variant uses Fabian’s (“MungeFloat”). The deltas are computed against Version 14c this time, to measure the speedup due to integer comparisons (rather than the speedup due to loop unrolling + integer comparisons).

The first thing we see is that indeed, using integer comparisons is measurably faster. This is not a big surprise since we saw the same in Version 7. But the gains are still very small (in particular, smaller than the theoretical 6% predicted by Ryg’s analysis) and to be honest I would probably still ignore them at this point. But using integers just for X’s is easy and doesn’t come with the tedious switch to integer SIMD intrinsics, so it’s probably not a big deal to keep them in that case.

On the other hand…

For some reason “encodeFloat” is faster on my home PC, while on my office PC it’s slower (and “MungeFloat” wins). This is unfortunate and slightly annoying. This is the kind of complications that I don’t mind dealing with if the gains are important, but for such small gains it starts to be a lot of trouble for minor rewards. I suppose I could simply pick up Ryg’s version because it’s more correct, and call it a day. That gives a nicely consistent overall X factor (13.37 vs 13.34) on the two machines.

And with this, we complete the port of Fabian’s assembly version to C++. Our new goal has been reached: we’re faster than version 14b now… at least on these two machines.

What we learnt:

An optimization that didn’t provide “significant gains” in the past might be worth revisiting after all the other, larger optimizations have been applied.

Similarly, we are slowly reaching a point where small differences in the setup code become measurable and worth investigating. There might be new optimization opportunities there. For example the question we previously dismissed about what kind of sorting algorithm we should use might soon come back to the table.

In any case, for now we reached our initial goal (make the code an order of magnitude faster), and we reached our secondary goal (make the C++ code faster than Ryg’s assembly version).

Surely we’re done now!?

How much longer can we keep this going?

Well… Don’t panic, but there is still a lot to do.

Stay tuned!

GitHub code for part 14d

Part 14c – that’s how I roll

Our goal today is to look at the details of what Fabian “Ryg” Giesen did in version 14b (an assembly version), and replicate them in our C++ unrolled version (14a) if possible.

First, let’s get one thing out of the way: I will not switch back to integer comparisons in this post. I like to do one optimization at a time, as you can probably tell by now, so I will leave this stuff for later. This means we can ignore the MungeFloat function and the integer-related changes in Fabian’s code.

Then, the first thing you can see is that the code has been separated in two distinct loops: a fast one (starting with the FastLoop label), and a safe one (starting with the CarefulLoop label).

One problem when unrolling the initial loop is that we don’t know ahead of time how many iterations we will have to do (it can stop at any time depending on the value of X we read from the buffer). It is much easier to unroll loops that are executed a known number of times when the loop starts.

Sometimes in this situation, one can use what I call the “radix sort strategy”: just use two passes. Count how many iterations or items you will have to deal with in a first pass, then do a second pass taking advantage of the knowledge. That’s what a radix-sort does, creating counters and histograms in a first pass. But that kind of approach does not work well here (or at least I didn’t manage to make it work).

Fabian’s approach is to just “look ahead” and check that the buffer still has at least 4 valid entries. If it does, he uses the “fast loop”. Otherwise he falls back to the “safe loop”, which is actually just our regular non-unrolled loop from version 12. In order to look ahead safely, the sentinel values are replicated as many times as we want to unroll the loop. This is a rather simple change in the non-assembly part of the code. First there:

SIMD_AABB_X* BoxListX = new SIMD_AABB_X[nb+5];

And then there:

BoxListX[nb+1].mMinX = ~0u;
BoxListX[nb+2].mMinX = ~0u;
BoxListX[nb+3].mMinX = ~0u;
BoxListX[nb+4].mMinX = ~0u;

That’s not assembly so no problem porting this bit to the C++ version.

Now, the “fast loop” is fast for three different reasons. First, it is unrolled four times, getting rid of the corresponding branching instructions – same as in our version 14a. Second, because we looked ahead and we know the four next input values are all valid, the tests against the MaxLimit value can also be removed. And finally, the idea we wanted to test at the end of 14a has also been implemented, i.e. we don’t need to increase the Offset value for each box (we can encode that directly into the address calculation).

At the end of the day, the core loop in Fabian’s version is thus:

// Unroll 0
movaps xmm3, xmmword ptr [edx+ecx*2+0] // Box1YZ
cmpnleps xmm3, xmm2
movmskps eax, xmm3
cmp eax, 0Ch
je FoundSlot0

// Unroll 1
movaps xmm3, xmmword ptr [edx+ecx*2+16] // Box1YZ
cmpnleps xmm3, xmm2
movmskps eax, xmm3
cmp eax, 0Ch
je FoundSlot1

// Unroll 2
movaps xmm3, xmmword ptr [edx+ecx*2+32] // Box1YZ
cmpnleps xmm3, xmm2
movmskps eax, xmm3
cmp eax, 0Ch
je FoundSlot2

// Unroll 3
movaps xmm3, xmmword ptr [edx+ecx*2+48] // Box1YZ
add ecx, 32 // Advance
cmpnleps xmm3, xmm2
movmskps eax, xmm3
cmp eax, 0Ch
jne FastLoop

That is only 5 instructions per box, compared to the 8 we got in version 14a. Color-coding it reveals what happened: in the same way that we moved the green blocks out of the loop in version 14a, Fabian’s version moved the blue blocks out of the (fast) loop. There is only one surviving blue instruction, to increase our offset only once for 4 boxes.

Pretty neat.

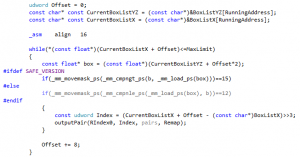
In our C++ code it would mean that the two lines marked in bold letters would / should vanish from our BLOCK macro:

Now another difference is that since we don’t increase the offset each time, we cannot jump to the same address at each stage of the unrolled code. You can see that in Fabian’s code, which jumps to different labels (FoundSlot0, FoundSlot1, FoundSlot2, or FastFoundOne). This is easy to replicate in C++ using goto. If you don’t want to use goto, well, good luck.

And that’s pretty much it. Let’s try to replicate this in C++.

As we said, replicating the setup code is trivial (it was already done in C++).

For the safe loop, we are actually going to use our previous unrolled VERSION3 from part 14a. In that respect this is an improvement over Fabian’s code: even our safe loop is unrolled. From an implementation perspective it couldn’t be more trivial: we just leave the code from part 14a as-is, and start writing another “fast” unrolled loop just before – the fallback to the safe loop happens naturally.

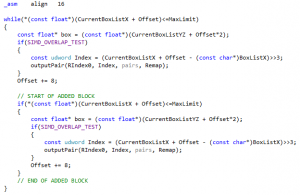
Now for our fast loop, we transform the BLOCK macro as expected from the previous analysis:

As we mentioned, the lines previously marked in bold vanished. Then we added two extra parameters: one (“x”) to include the offset directly in the address calculation (as we wanted to do at the end of version 14a, and as is done Fabian’s code), and another one (“label”) to make the code jump to a different address like in the assembly version.

Now, one small improvement over Fabian’s code is that we will put the “overlap found” code before the fast loop starts, not after it ends. That’s what we did in version 14a already, and it saves one jump.

Another improvement is that we’re going to unroll 5 times instead of 4, as we did in version 14a. That’s where using BLOCK macros pays off: unrolling one more time is easy and doesn’t expand the code too much.

After all is said and done, the code becomes:

I know what you’re going to say (hell, I know what you did say after I posted a preview of part 14): it looks horrible.

Sure, sure. But once again: see through the C++, and check out the disassembly for our fast loop:

001E30B0 comiss xmm2,dword ptr [edi+esi+28h]
001E30B5 jb StartLoop4+12Fh (01E31D4h)
{
BLOCK4(0, FoundOverlap0)
001E30BB movaps xmm0,xmmword ptr [ecx-20h]
001E30BF cmpnltps xmm0,xmm1
001E30C3 movmskps eax,xmm0
001E30C6 cmp eax,0Fh
001E30C9 je StartLoop4+9Bh (01E3140h)
BLOCK4(8, FoundOverlap1)
001E30CB movaps xmm0,xmmword ptr [ecx-10h]
001E30CF cmpnltps xmm0,xmm1
001E30D3 movmskps eax,xmm0
001E30D6 cmp eax,0Fh
001E30D9 je StartLoop4+8Bh (01E3130h)
BLOCK4(16, FoundOverlap2)
001E30DB movaps xmm0,xmmword ptr [ecx]
001E30DE cmpnltps xmm0,xmm1
001E30E2 movmskps eax,xmm0
001E30E5 cmp eax,0Fh
001E30E8 je StartLoop4+7Bh (01E3120h)
BLOCK4(24, FoundOverlap3)
001E30EA movaps xmm0,xmmword ptr [ecx+10h]
001E30EE cmpnltps xmm0,xmm1
001E30F2 movmskps eax,xmm0
001E30F5 cmp eax,0Fh
001E30F8 je StartLoop4+6Dh (01E3112h)
// BLOCK4(32, FoundOverlap4)
Offset += 40;
BLOCK4(-8, FoundOverlap)
001E30FA movaps xmm0,xmmword ptr [ecx+20h]
001E30FE add ecx,50h
001E3101 cmpnltps xmm0,xmm1
001E3105 add esi,28h
001E3108 movmskps eax,xmm0
001E310B cmp eax,0Fh
001E310E jne StartLoop4+0Bh (01E30B0h)
}
001E3110 jmp StartLoop4+0ABh (01E3150h)

That’s pretty much perfect.

We get an initial comiss instruction instead of cmp because we didn’t bother switching X’s to integers, and we see the loop has been unrolled 5 times instead of 4, but other than that it’s virtually the same as Fabian’s code, which is what we wanted.

We get the following results:

The deltas in the results are compared to version 13, similar to what we did for version 14a.

Thanks to our small improvements, this new version is actually faster than version 14b (at least on my machines) – without using integers! As a bonus, this is based on the “safe” version 14a rather than the “unsafe” version 12.

What we learnt:

Once again the assembly version showed us the way. I am not sure I would have “seen” how to do this one without an assembly model I could copy.

Ugly C++ can generate pretty good looking assembly – and vice versa.

Unrolling is like SIMD: tricky. It’s easy to get gains from some basic unrolling but writing the optimal unrolled loop is quite another story.

Stay tuned. In the next post we will complete our port of Fabian’s code to C++, and revisit integer comparisons.

GitHub code for part 14c

Part 14b – Ryg rolling

After I wrote about this project on Twitter, Fabian “Ryg” Giesen picked it up and made it his own. For those who don’t know him, Fabian works for RAD Game Tools and used to be / still is a member of Farbrausch. In other words, we share the same demo-scene roots. And thus, it is probably not a surprise that he began hacking the box-pruning project after I posted version 12 (the assembly version).

Now, at the end of part 14a we thought we could still improve the unrolled code by taking advantage of the address calculation to get rid of some more instructions. As it turns out, Fabian’s code does that already.

And much more.

Since he was kind enough to write some notes about the whole thing, I will just copy-paste his own explanations here. This is based on my assembly version (i.e. box pruning version 12), and this is just his initial attempt at optimizing it. He did a lot more than this afterwards. But let’s do one thing at a time here.

In his own words:

—-

Brief explanation what I did to get the speed-up, and the thought process behind it.

The original code went:

My first suggestion was to restructure the loop slightly so the hot “no overlap” path is straight-line and the cold “found overlap” path has the extra jumps. This can help instruction fetch behavior, although in this case it didn’t make a difference. Nevertheless, I’ll do it here because it makes things easier to follow:

Alright, so that’s a nice, sweet, simple loop. Now a lot of people will tell you that out-of-order cores are hard to optimize for since they’re “unpredictable” or “fuzzy” or whatever. I disagree: optimizing for out-of-order cores is *easy* and far less tedious than say manual scheduling for in-order machines is. It’s true that for OoO, you can’t just give a fixed “clock cycles per iteration” number, but the same thing is already true for *anything* with a cache, so who are we kidding? The reality of the situation is that while predicting the exact flow uops are gonna take through the machine is hard (and also fairly pointless unless you’re trying to build an exact pipeline simulator), quantifying the overall statistical behavior of loops on OoO cores is often easier than it is for in-order machines. Because for nice simple loops like this, it boils down to operation counting - total number of instructions, and total amount of work going to different types of functional units. We don’t need to worry about scheduling; the cores can take care of that themselves, and the loop above has no tricky data dependencies between iterations (the only inter-iteration change is the “add ecx, 8″, which doesn’t depend on anything else in the loop) so everything is gonna work fine on that front. So, on to the counting. I’m counting two things here: 1. “fused domain” uops (to a first-order approximation, this means “instructions as broken down by the CPU front-end”) and 2. un-fused uops going to specific groups of functional units (”ports”), which is what the CPU back-end deals with. When I write “unfused p0″, I mean an unfused uop that has to go to port 0. “unfused 1 p23″ is an unfused uop that can go to ports 2 or 3 (whichever happens to be free). I’m using stats for the i7-2600K in my machine (Intel Sandy Bridge); newer CPUs have slightly different (but still similar) breakdowns. Now without further ado, we have:

(yes, the pair of x86 instructions cmp+je combines into one fused uop.)

Fused uops are the currency the CPU frontend deals in. It can process at most 4 of these per cycle, under ideal conditions, although in practice (for various reasons) it’s generally hard to average much more than 3 fused uops/cycle unless the loop is relatively short (which, luckily, this one is). All the ports can accept one instruction per cycle.

So total, we have:

And of that total, the actual box pruning test (the first 5 x86 instructions) are 4 fused uops, 3 unfused p015 and 1 unfused p23 - a single cycle’s worth of work. In other words, we spend more than half of our execution bandwidth on loop overhead. That’s no good.

Hence, unroll 4x. With that, provided there *are* at least 4 boxes to test against in the current cluster, we end up with:

Our bottleneck are once again ports 0,1,5, but they now process 4 candidate pairs in 5.33 cycles worth of work, whereas they took 9.33 cycles worth of work before. So from that analysis, we expect something like a 42.8% reduction in execution time, theoretical. Actual observed reduction was 34.4% on my home i7-2600K (12038 Kcyc -> 7893 Kcyc) and 42.9% on my work i7-3770S (8990 Kcyc -> 5131 Kcyc). So the Sandy Bridge i7-2600K also runs into some other limits not accounted for in this (very simplistic!) analysis whereas the i7-3770S behaves *exactly* as predicted.

The other tweak I tried later was to switch things around so the box X coordinates are converted to integers. The issue is our 2-fused-uop COMISS, which we’d like to replace with a 1-fused-uop compare. Not only is the integer version fewer uops, the CMP uop is also p015 instead of the more constrained p0+p1 for COMISS.

What would we expect from that? Our new totals are:

From the back-of-the-envelope estimate, we now go from purely backend limited to simultaneously backend and frontend limited, and we’d expect to go from about 5.33 cycles/iter to 5 cycles/iter, for a 6.2% reduction.

And indeed, on my work i7-3770S, this change gets us from 5131 Kcyc -> 4762 Kcyc, reducing the cycle count by 7.2%. Close enough, and actually a bit better than expected!

This example happens to work out very nicely (since it has a lot of arithmetic and few branch mispredictions or cache misses), but the same general ideas apply elsewhere. Who says that out-of-order cores are so hard to predict?

—-

Right. Thank you Fabian. That was certainly a… rigorous explanation.

Here are a few comments that come to mind:

• It is certainly true that manually pairing the assembly code for the U and V pipelines of the first Pentiums (which I did a lot in the past) was far more tedious than letting the out-of-order processors deal with it for me.
• It boils down to operation counting indeed. That’s what we noticed in the previous posts: reducing the total number of instructions has a measurable impact on performance in this case.
• I did try to restructure the loop to remove the jump from the hot path, but as you noticed as well it didn’t make any difference. But as a side-effect of another goal (reducing the size of the main loop), the hot path became jump-free in version 14a anyway.
• Using integers is what we tried in version 7 already. While we did measure gains, they were too small to matter and we ignored them. That being said, version 7 took 40000+ KCycles… so the gains might have been small compared to the total cost at the time, but if we still get the same gains today it might be a different story. In other words, going from 5131 to 4762 K-Cycles is just a 369 K-Cycles gain: peanuts compared to 40000, but probably worth it compared to 4000. And yes, using integers for X’s only may also be a better idea than using them for everything. So we will revisit this and see what happens in the C++ version.

In any case, here are the timings for Ryg’s version on my machines:

The Delta and Speedup columns are computed between Ryg’s version and the previous best assembly version. The Timings and Overall X factor columns are absolute values that you can use to compare Ryg’s version to our initial C++ unrolled version (14a). The comparisons are not entirely apple-to-apple:

• Versions 12 and 14b are “unsafe”, version 14a is “safe”.
• Versions 12 and 14b are assembly, version 14a is C++.
• Version 14b does more than unrolling the loop, it also switches some floats to integers.

So the comparisons might not be entirely “fair” but it doesn’t matter: they give a good idea of what kind of performance we can achieve in “ideal” conditions where the compiler doesn’t get in the way.

It gives a target performance number to reach.

And that’s perfect really because we just reached our previous performance target (10x!) in the previous post.

So we need a new one. Perfect timing to send me new timings.

Well, gentlemen, here it is: our new goal is to reach the same performance as Ryg’s unrolled assembly version, but using only C++ / intrinsics – to keep things somewhat portable.

This is what we will try to do next time.

Stay tuned!

What we learnt:

It is always a good idea to make your code public and publish your results. More often than not you get good feedback and learn new things in return. Sometimes you even learn how to make your code go faster.

Ex-scene coders rule. (Well we knew that already, didn’t we?)

GitHub code for part 14b

Part 14a – loop unrolling

The main codepath from version 13 had only 9 assembly instructions, and there wasn’t much room left for improvements in terms of reducing the instructions count. Nonetheless we saw that doing so had a measurable impact on performance. At the same time, we identified a problem with the code alignment of our main loop, which was apparently not properly handled by the compiler.

In that situation, a typical thing to do is unroll the loop. It reduces the amount of branch instructions needed to loop. And of course, misaligned loops are less of a problem if we loop less.

Loop unrolling is pretty much the oldest trick in the book, but it still has its place today. On the Atari ST for example, things were pretty simple: any removed instruction gave an immediate performance gain. There were no cache effects, the code always took a very predictable amount of time, and the more you unrolled, the faster it became. No surprises. This led to certain abuses where loops got unrolled thousands of times, creating huge blocks of code that quickly consumed all the available memory. In the old days of TASM on PC, the REPT / ENDM directives could be used to unroll the code and achieve similar speedups.

These days however, processors are a little bit more complicated, subtle, unpredictable. And loop unrolling is not always a win. In particular, if you unroll too much, the code can become slower. The previously mentioned Intel optimization manual has some details about this, in chapter 3.4.1.7. It became more difficult to foresee and explain, but the basic strategy remains as simple as in the past, as we will see just now.

Our code at the end of version 13 looked like this:

If we hide the safe/unsafe version business behind a trivial SIMD_OVERLAP_TEST macro, unrolling that loop twice can be as easy as simply copy-pasting the inner block, like this (VERSION1_UNROLL2 in the code):

This is as easy as it gets, and in this specific case it already provides performance gains! However, unroll it exactly the same way but three times (VERSION1_UNROLL3 in the code) and it becomes slower again. That’s a neat illustration of what we said just before: unrolling the loop too much can hurt performance. Here is a quick summary of timings for the office PC, safe version (new entries in bold letters):

So what is wrong with unrolling the loop three times here? Looking at the disassembly reveals a potential problem: the part that outputs the pair is replicated three times inside the loop, making the code quite large. The Intel optimization manual warns about this, for example stating that “unrolling can be harmful if the unrolled loop no longer fits in the trace cache”. Whether this is what actually happens here or not is not terribly relevant: the important point is that it gives us a new theory to test, and a new direction for our next attempt. Refactoring the code so that the block that outputs the pair moves out of the loop gives birth to version 2, here unrolled twice (VERSION2_UNROLL2):

As you can see it is very similar to the previous version: the only difference is that the part where an overlap is found has been clearly moved out of the way, before the loop even starts. When an overlap is found, we jump there and fallback to the start of the loop.

The presence of goto should not be frowned upon: as I’ve said before, you must see through the C++, and consider the generated assembly. Generally speaking the assembly is shock-full of jump instructions (i.e. goto) anyway. And after version 13 where we tried to mimic the desired assembly in C++, the appearance of goto here should not be a surprise.

In any case: it’s 2017, I don’t have the time or energy to discuss once again whether goto should be considered harmful. It’s a tool. It serves a purpose. If you can avoid it, do so, but if you cannot, don’t be ashamed. People for whom this is a deal-breaker can stick to version 13. Or maybe look out for a future version in a future post that would perhaps drop them – I don’t know yet.

Now, as we did with version 1, we can try to unroll the loop twice (VERSION2_UNROLL2) and three times (VERSION2_UNROLL3). The results for the office PC / safe version are:

All “Version 14a” entries are compared to Version 13 here, not to each-other.

What we see seems to confirm the theory. Looking at the disassembly, the output-pair-related code did move out of the loop, making it tighter overall. As a result, unrolling version 2 three times still gives performance gains. But if we try to unroll it one more time (VERSION2_UNROLL4), we see the performance drop again. It’s the same pattern as with version 1: at some point the unrolled code apparently becomes too large and starts to be slower.

In any case, the assembly for VERSION2_UNROLL3 looks pretty good:

01103002 comiss xmm1,dword ptr [edi+esi]
01103006 jb LoopStart+96h (01103098h)
0110300C movaps xmm0,xmmword ptr [ecx+esi*2]
01103010 cmpnltps xmm0,xmm2
01103014 movmskps eax,xmm0
01103017 cmp eax,0Fh
0110301A je LoopStart+51h (01103053h)
0110301C add esi,8

0110301F comiss xmm1,dword ptr [edi+esi]
01103023 jb LoopStart+96h (01103098h)
01103025 movaps xmm0,xmmword ptr [ecx+esi*2]
01103029 cmpnltps xmm0,xmm2
0110302D movmskps eax,xmm0
01103030 cmp eax,0Fh
01103033 je LoopStart+51h (01103053h)
01103035 add esi,8

01103038 comiss xmm1,dword ptr [edi+esi]
0110303C jb LoopStart+96h (01103098h)
0110303E movaps xmm0,xmmword ptr [ecx+esi*2]
01103042 cmpnltps xmm0,xmm2
01103046 movmskps eax,xmm0
01103049 cmp eax,0Fh
0110304C je LoopStart+51h (01103053h)
0110304E add esi,8

01103051 jmp LoopStart (01103002h)

It is color-coded the same way as in previous posts, to show where all the bits and pieces moved. The compiler did exactly what we wanted, unrolling the code three times in the obvious way. As expected, the green block from version 13 (the part that outputs pairs) moved out of the loop. Perhaps as a result, the compiler finally stopped spilling our registers to the stack, and we now use 8 instructions per test (as opposed to 9 in version 13).

So the good news is that we found an easy way to make the code faster. And in fact, this version is a significant milestone: we just reached our 10X speedup target!

The bad news is that this code size limit might vary from one platform to the next, so without testing on each of them there is no guarantee that what we are doing here actually helps. It might very well be the case that VERSION2_UNROLL3 is faster on PC for example, but slower on some console – or on some other PC with another processor. In that respect, loop unrolling is a perhaps more fragile and debatable optimization than things like avoiding cache misses, etc, which are more universally beneficial. Still, we started the questionable optimizations with version 13 already, and this isn’t worse.

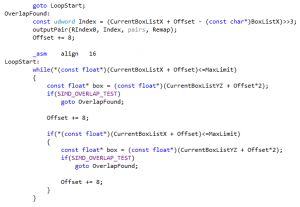
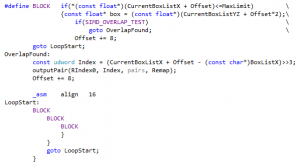
To test various amount of unrolling more easily on each platform, it is perhaps useful to capture the common bits in a macro. This is what VERSION2_UNROLL does, and it admittedly starts to look slightly evil:

The last goto has been added because the initial while directive disappeared, replaced with the if within the BLOCK macro. Amazingly, this “innocent change” is enough to significantly change the generated assembly. Fortunately it doesn’t change the timings - this form is perhaps even a tiny bit faster:

It looks quite fine.

However… running the same tests on the home PC exposes the main issue with loop unrolling:

The results are similar…. yet so subtly different. In particular:

• Unrolling version 2 four times (VERSION2_UNROLL4) still provides clear performance gains, while it made the code slower on the office PC.
• VERSION2_UNROLL4 and VERSION2_UNROLL are almost the same speed… even though one is unrolled one more time! In theory VERSION2_UNROLL should be equivalent to VERSION2_UNROLL3 (as on the office PC). But for some unknown reason it is clearly faster here.

These observations gave birth to a new version, VERSION3, which copies VERSION2_UNROLL but unrolls the loop five times – the unrolling limit on the home PC.

And lo and behold…

That’s quite a speedup! I cannot explain it but I’ll take it. Running this new version on the office PC gives:

So the gains for VERSION3 are minimal on this machine, but we got lucky: at least this version isn’t slower. Sometimes you end up with different “best” versions on different machines. That is probably the biggest problem with loop unrolling: until you test “everywhere”, selecting a “winner” is a bit like a shot in the dark.

What one can do in difficult cases is to look at the numbers: sometimes the best version on one machine is still slower (in absolute number of cycles) than sub-optimal versions on another machine. So one strategy here is to select the fastest version on the slowest machine, and accept whatever results it gives on the faster machine. That way you make sure that your choices don’t penalize the machines that need the optimizations the most.

In our case here, we got lucky anyway: VERSION3 wins, and this is the version we will continue to work with.

But what is there left to do anyway?

Well, looking at the previous disassembly, another obvious thing to try pops up: increasing esi for each box seems useless. We could use the relevant offsets in the address calculations, increase esi only once in the end, thus saving some extra instructions and making the code tighter.

That’s the plan for the next post. However, before tackling this in the C++ version, we will revisit the assembly version thanks to a special guest.

What we learnt:

Loop unrolling still has its uses in 2017.

But it is a lot trickier than in the past. The optimal amount of unrolling varies from one machine to the next, and unrolling too much can actually make the code run slower.

We reached our 10X speedup target!

GitHub code for part 14a

FYI

http://www.roadtovr.com/video-nvidia-demos-physx-rigid-body-gpu-physics/