PhysX tip: use tight convex bounds
There is a new flag in PhysX 3.4 that tells the system to use tight bounds for convexes: PxConvexMeshGeometryFlag::eTIGHT_BOUNDS.
Use it.
Until now PhysX used a fast O(1) piece of code to update the AABB of a convex mesh, from its precomputed local AABB and the current world transform. That one’s a classic from the GD-Algorithms days, and I remember also spotting it in Charles Bloom’s public code years and years ago. If you want the details, see for example this file in the PEEL distro:
.\PEEL\Physics\Ice\APIs\Ice\IceMaths\IceAABB.h
And then look up the “Rotate” function, implemented there both for min/max and center/extents AABBs. This stuff is from 2000 or before, nothing new here.
There is no problem with this “Rotate” function: it’s great, we’ve been using it for more than a decade, and we’re still using it.
However, it obviously does not create the tightest possible AABB, since it only knows about the local un-transformed bounds, and it doesn’t know anything about the object contained within these bounds. That’s why for simple shapes like boxes or capsules we don’t use it: instead we directly recompute the sphere or capsule’s bounds from its data and current pose. This is just as fast, but also provides tighter bounds.
For convexes though, we never tried that, because computing tight bounds for them was more tedious. You either need to use brute-force and iterate over all vertices (which is a potentially expensive O(N) approach), or you need to do something more complex like maybe hill-climbing, etc: basically the same stuff as for GJK really, which has pros and cons I won’t go into right now.
Long story short: in PhysX 3.4 we tried the brute-force approach, and found that it significantly improves both performance and memory usage in scenes with piles of convex objects. The number of vertices in a convex is limited to 256 in PhysX, so there’s a limit to how expensive the computation can be, and we found it reasonable (iterating over vertices in a linear array is cache & SIMD friendly, so the worst case isn’t that bad).
Here are some results using PEEL’s “ConvexGalore2″ test scene. It’s a giant pile of convex objects falling, and it looks like this:
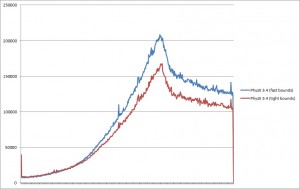
Here are the performance results with and without tight bounds. Blue is with the default PhysX settings, red is with PxConvexMeshGeometryFlag::eTIGHT_BOUNDS. There’s a pretty clear winner here:
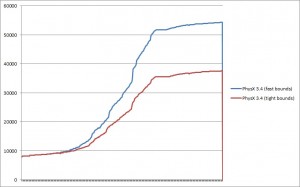
It also improves memory usage, since the tighter bounds mean less candidate pairs are generated from the broadphase, etc. This is again a clear win:
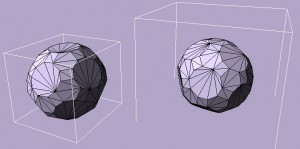
Granted: computing the bounds becomes more expensive, and if you have convex objects that don’t ever go close to other convex objects, using the flag might reduce performance overall. But I’d say that all things considered it’s one of these easy flags that you should just use all the time. It’s a small price to pay for potentially big gains. Visually the difference between the regular and tight bounds can be quite dramatic, as you can see for example here: