Coder Corner

Part 6b – less cache misses

Last time we took care of our input data, and packed it in a nice flat linear array. This is necessary but not sufficient to guarantee high performance: it only helps if you actually read that input array sequentially. But if you read random boxes within the input array, you still get cache misses.

But do we still get cache misses? We got great speedups with our previous change so aren’t we done? How do we know if there is more to gain from “the same” optimization?

One way is simply to look at the code. With some experience you can relatively easily spot the potential problems and “see” if the code is sound or not.

Another way would be to use a profiler like V-Tune, and check how many cache misses you get in that function.

And sometimes you can simply design small experiments, small tests that artificially remove the potential problems. If the performance doesn’t change, then you know you’re good, nothing left to do. If the performance does change, then you know you have some more work ahead of you.

This probably sounds a bit abstract so let me show you what I mean. The code is like this now:

So we’re going to read from this badly-named “list” array. We look for “list” in the code. We first find this:

This reads the array sequentially, this is theoretically optimal, so no problem here. Granted: we don’t use all the data in the cache line we just fetched, but let’s ignore this. For now we are just checking whether we read the array sequentially or in random order.

Next we find this:

With:

And “Sorted” is the output of the radix sort, which sorted boxes along the X axis.

Well this one is not good. The radix implementation is for a “rank sorter”, i.e. it returns sorted indices of input bounds. But it does not sort the input array itself (contrary to what std::sort would do, for example). This means that we keep reading random boxes in the middle of the box-pruning loop. Oops.

And the same problem occurs for Index1 later on:

So this is what I mentioned above: you read the code, and you can easily spot theoretical problems.

And then you can sometimes design tests to artificially remove the problem and see if performance changes. In this case we’re lucky because it’s easy to do: we can just pre-sort the input array (the bounds) before calling the box-pruning function. That way the sorting inside the function will have no effect, the radix sort will return an identity permutation, the code will read the input array sequentially, and we will see how much time we waste in cache misses.

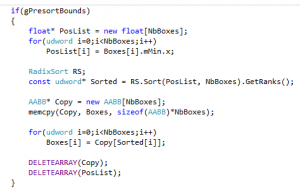
Quickly said, quickly done, the change is just like this in Main.cpp:

Change gPresortBounds from false to true, run the test again… and….

Home PC:

Complete test (brute force): found 11811 intersections in 355897 K-cycles.

Complete test (box pruning): found 11811 intersections in 46586 K-cycles.

Office PC:

Complete test (brute force): found 11811 intersections in 312868 K-cycles.

Complete test (box pruning): found 11811 intersections in 49315 K-cycles.

Wo-ah.

Now that’s interesting. The function became faster again. This means that we are still suffering from cache misses out there, and that there is more to do to address this issue.

It is also a great example of why data-oriented design matters: the code did not change at all. It is the exact same function as before, same number of instructions, same position in the executable. It computes the same thing, returns the same number of overlapping pairs.

But somehow it’s 15% / 20% faster, just because we reorganized the input data. Ignore this, focus only on the code, and that’s the amount of performance you leave on the table in this case.

On a side note, we saw this kind of things in the past, in different contexts. For example triangle lists reorganized to take advantage of the vertex cache were faster to render - sometimes faster than strips. Even on older machines: making the code run faster by just changing the data is very reminiscent of what Leonard / Oxygene reported when working on his 16*16 “sprite record” demos on Atari ST. Several times in these experiments the Atari ST code didn’t change at all, but he was able to display more and more sprites by improving his “data builder” (a tool running on a PC). This had nothing to do with cache misses, but it was the same observation: you get the best results by optimizing both the code and the data. In his case, the data was not even optimized on the same machine/architecture.

So, anyway: we identified the problem. Now how do we solve it?

Well, the obvious way: we just create a secondary bounds array, sorted in the desired order, and we parse that sorted array instead of the original one. Basically we simply replicate what we did above to presort bounds, inside the box pruning function.

So, yes, we need more memory. And yes, the setup code becomes more complex (but it was not the bottleneck at all, remember? So it doesn’t matter).

On the other hand, now that the array itself is sorted, there is no need to work with the sorted indices anymore: they will always be the identity permutation. So the setup code becomes more complex but the inner loop’s code can actually be further simplified.

One complication is that we need to introduce a remapping between the user’s box indices and our now entirely sequential internal box indices. Fortunately we already have the remap table: it is the same as the sorted indices returned by the radix sort! So it all fits perfectly together and the only thing we need to do is remap the box indices after an overlap has been found, before writing them to the output buffer. In other words: we removed indirections in the frequent case (for each parsed box), and added indirections in the infrequent case (when an overlap is actually found).

The results speak for themselves.

Home PC:

Complete test (brute force): found 11811 intersections in 781350 K-cycles.
45584 K-cycles.
44734 K-cycles.
41679 K-cycles.
41810 K-cycles.
41654 K-cycles.
41623 K-cycles.
41634 K-cycles.
41605 K-cycles.
41779 K-cycles.
41633 K-cycles.
42037 K-cycles.
41752 K-cycles.
41836 K-cycles.
41639 K-cycles.
41618 K-cycles.
41636 K-cycles.
Complete test (box pruning): found 11811 intersections in 41605 K-cycles.

Office PC:

Complete test (brute force): found 11811 intersections in 813615 K-cycles.
46985 K-cycles.
46282 K-cycles.
47889 K-cycles.
47757 K-cycles.
55044 K-cycles.
52660 K-cycles.
47923 K-cycles.
53199 K-cycles.
47410 K-cycles.
46192 K-cycles.
45860 K-cycles.
46140 K-cycles.
45634 K-cycles.
46274 K-cycles.
47077 K-cycles.
46284 K-cycles.
Complete test (box pruning): found 11811 intersections in 45634 K-cycles.

The gains are summarized here:

This is even faster than what we got during our previous experiment with pre-sorted bounds. Which means that not only we took care of the cache misses, but also the extra simplifications of the main loop provided additional gains. Bonus!

And with that, we became 2X faster than the version we started from. That’s a milestone.

What we learnt:

The same as in the previous post, but it’s so important it’s worth repeating: cache misses are more costly than anything else. If you can only optimize one thing, that’s what you should focus on.

Before we wrap this one up, let’s come back to the loss of genericity we mentioned before. At the end of part 5 we said that we could get back our generic version for no additional cost. That is, we could put back the user-defined axes and don’t pay a performance price for it.

It should be clear why this is the case. We are now parsing internal buffers in the main loop, instead of the user-provided source array. So we could very easily flip the box coordinates while filling up these internal buffers, in the setup code. The main inner loop would remain untouched, so it would give back the user-defined axes virtually for free.

So that’s one loose end taken care of. But there is another big one left, also mentioned in part 5: SIMD.

We will slowly move towards it in next post.

GitHub code for part 6b

This entry was posted on Tuesday, February 14th, 2017 at 6:20 am and is filed under Physics, Programming. You can follow any responses to this entry through the RSS 2.0 feed. Both comments and pings are currently closed.