Coder Corner

Part 17 – PhysX lessons

In this series, we have been looking at fairly low-level optimizations so far. For example reducing the number of instructions, reducing the amount of cache-misses, aligning the data, switching to SIMD, etc. Grosso modo, we have improved the implementation of an algorithm.

But that was only the first part. In this post we start investigating the other side of the story: high-level optimizations, i.e. improvements to the algorithm itself.

Multi Box Pruning

In part 1, I briefly explained where “box-pruning” came from. The details are available in the sweep-and-prune (SAP) document that I wrote a decade ago now. That paper also explains the issues with the traditional SAP algorithm, and introduces the “multi-SAP” idea to address them.

The box-pruning algorithm we have been optimizing so far is also a SAP variant, and as such it suffers from similar issues. For example box pruning also suffers from “useless interactions with far away objects”, as described in page 17 of the SAP document. This is easy to see: imagine a vertical stack of equally-sized boxes, with either Y or Z as the up/vertical axis. Our code projects the boxes on the X axis. So all “projected” values end up equal (all min values are the same, all max values are the same). The “pruning power” of the first loop drops to zero. The second loop basically degenerates to our brute-force version. This is of course an extreme example that would not happen exactly as-is in practice, but the important point is that mini-versions of that example do happen all over the place in regular cases, making the broadphase less efficient than it could be.

The “multi-SAP” solution used a grid over the 3D world. Objects were assigned to grid cells, and a regular SAP was used in each cell. By design faraway objects then ended up in faraway cells, reducing the amount of aforementioned useless interactions.

We added something similar to multi-SAP in PhysX starting from version 3.3. It was called “MBP”, for Multi Box Pruning. As the name suggests, it was basically the multi-SAP idea applied to a box-pruning algorithm rather than applied to a regular incremental sweep-and-prune. It turns out that algorithmic improvements to SAP also work for box-pruning.

The PhysX implementation differs from the Multi-SAP implementation detailed in the SAP document. For example it does not use a grid of non-overlapping cells. Instead, it needs user-provided broadphase regions, which can overlap each other. And each object can belong to an arbitrary number of cells. But other than these implementation details, the basics are the same as what I described ten years ago: the overlaps are found separately for each region, they are added to a shared pair manager structure, and some extra management code is needed to deal with objects crossing regions.

In our box pruning project here, we do not have any API for updating or removing objects from the structures: we effectively do the PhysX “add object” operations each time. This has pros and cons.

The bad thing about this is that it is not optimal in terms of performance. In all our timings and tests so far, we have always been recomputing the exact same set of overlaps each time – each “frame” if you want. A good broadphase would take advantage of this, notice that objects have not changed from one call to the next, and only the first call would actually compute the overlaps. Subsequent calls would be either free (as for the incremental SAP in PhysX) or at least significantly cheaper (as for MBP in PhysX).

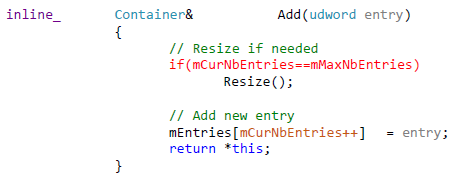
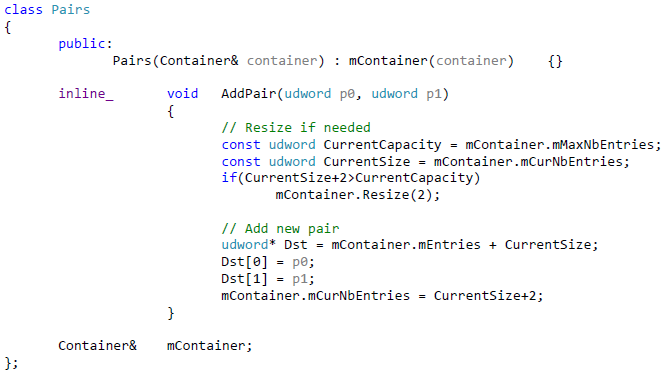
On the other hand, the good thing about this is that we do not need the previously mentioned “extra management code” from MBP in our little project here. To replicate the “add object” codepath from MBP, all we would need is some grid cells and a pair manager, i.e. for example a hash-map. Recall that so far we added overlapping pairs to a simple dynamic array (like an std::vector<Pair>). In MBP, an object touching two separate grid cells is added to both cells. So when computing the overlaps in each cell individually, it is possible to find the same overlapping pair multiple times. Some mechanism is needed to filter out duplicates, and in PhysX we do this by adding pairs to a shared hash-map / hash-set.

We do not have user-defined broadphase regions in this project, but we could try to compute some of them automatically. Here is how it would work in 2D:

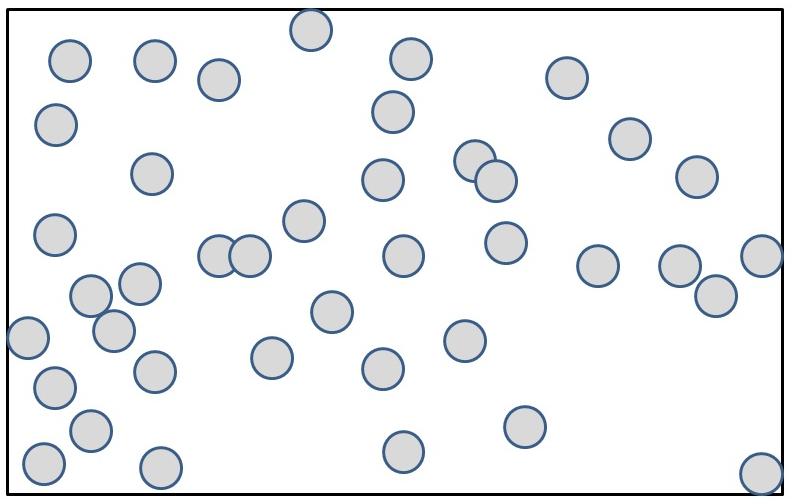
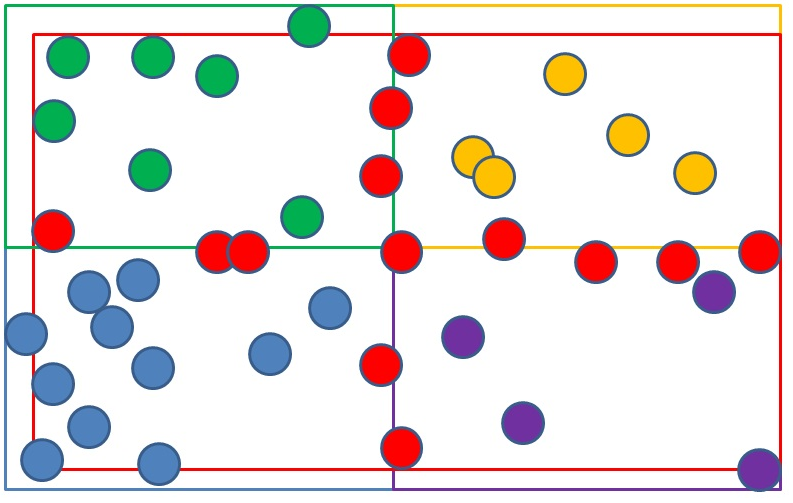
a) Start with a bunch of objects (the blue spheres). Compute the black bounding box around them.

Picture 1: compute the AABB around all objects

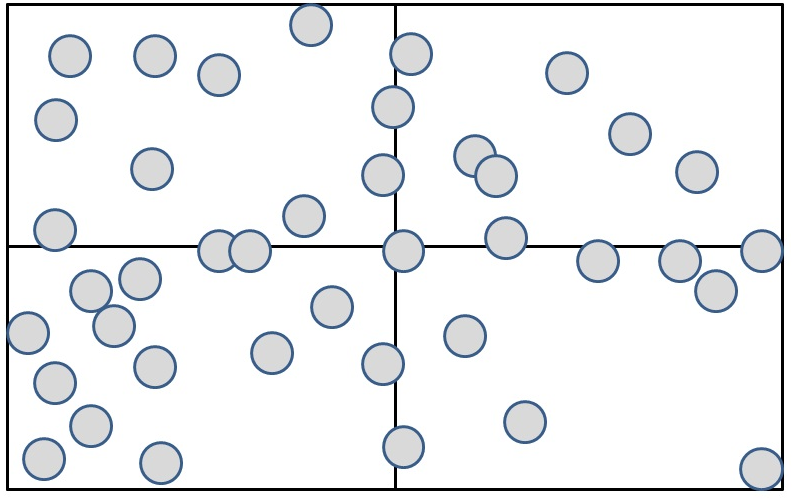
b) Subdivide the bounding box computed in the first step. This gives 4 broadphase regions.

Picture 2: subdivide the AABB into 4 regions

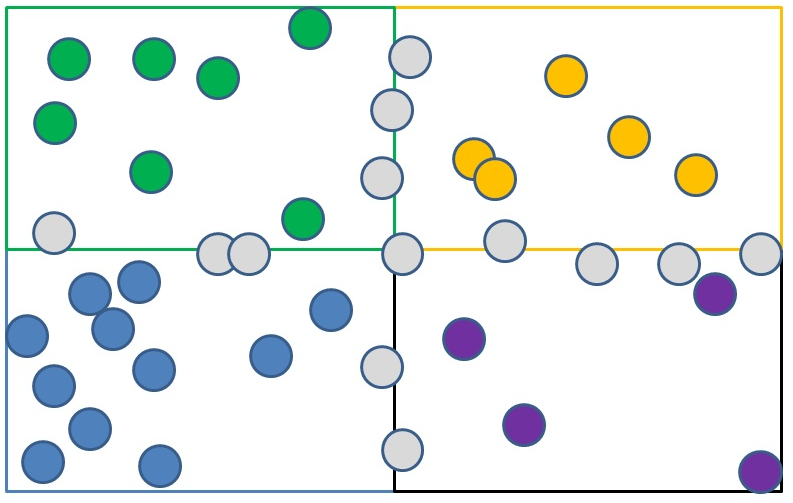
c) Classify objects depending on which region they fall in. Green objects go into the 1st region, yellow objects into the 2nd region, blue objects into the 3rd region, magenta objects into the 4th region.

Picture 3: assign objects to regions

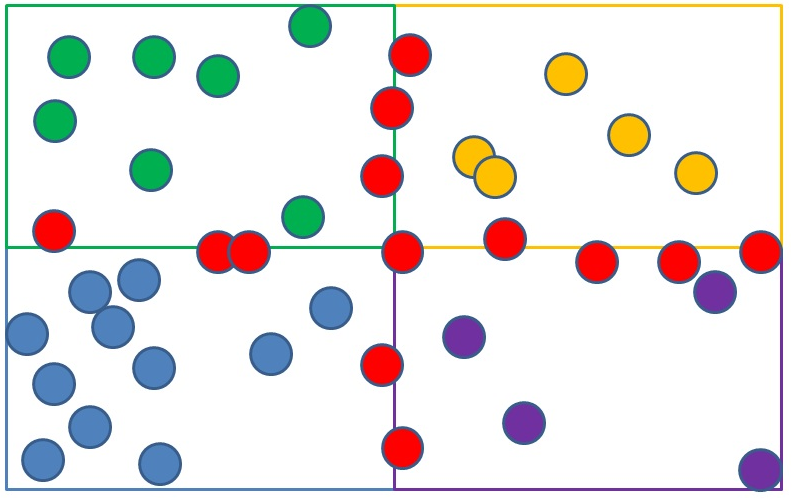
d) The remaining red objects touch multiple regions. In PhysX using MBP, each red object is duplicated in the system, added to each region it touches.

Picture 4: objects touching multiple regions are duplicated

To find the overlaps, we then perform 4 “completeBoxPruning” calls (one for each region). Colliding pairs are added to a shared hash-map, which by nature filters out duplicates. So for example a pair of touching red objects, like the one overlapping the green and blue regions in the picture, will be reported twice by both the green and blue broadphase regions. But since we add the pair to a shared (unique) hash-map, the second addition has no effect.

So we could replicate this in our box-pruning project. We could implement a hash-map (or reuse one that I released on my website years ago) and give this a try. But adding the same objects to different regions also leads to increased memory usage. And the resulting code quickly becomes unpleasant.

So instead, in this project we’re going to try something different.

Bucket pruner

There is another interesting data structure in PhysX called a “bucket pruner”. This is used in the context of scene queries rather than broadphase (i.e. raycasts, overlap tests, etc). Long story short, we needed something that was faster to build than a regular AABB tree, while providing some speedup compared to testing each objects individually.

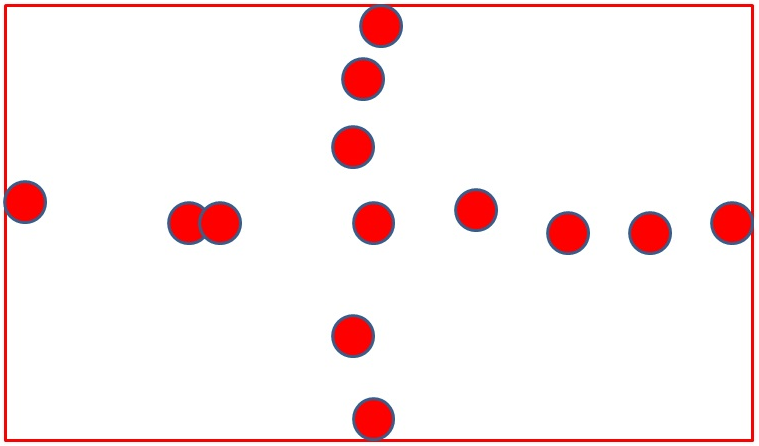
Roughly speaking, it is built exactly like what we just described before. The 4 previously defined broadphase regions are what we call the “natural buckets”. But the structure handles the red objects in a different way: they are not duplicated and added to existing regions; instead they go to a special 5th bucket named “cross bucket”.

Picture 5: put duplicated objects in their own region

It is called “cross bucket” (or boundary bucket) because objects inside it often form a cross-like shape. It also contains objects that cross a boundary, so the name has a double meaning.

Picture 6: the cross bucket

In PhysX the classification process is then repeated again for each bucket (with special subdivision rules for the cross-bucket). This is done recursively a fixed number of times. At the end of the day the bucket pruner is a mix between a BVH and a spatial-partitioning structure: we compute bounds around objects as in a BVH, but we divide the resulting space in equally-sized parts as in a spatial partitioning structure (e.g. a quadtree). Since we do not do any clever analysis to find the best splitting points, and because we only recurse a small fixed amount of times, the whole thing is quick to build – much quicker than a regular AABB tree for example.

Now, how does that help us for box-pruning?

This is where all the pieces of the puzzle come together, and my cunning plan is revealed.

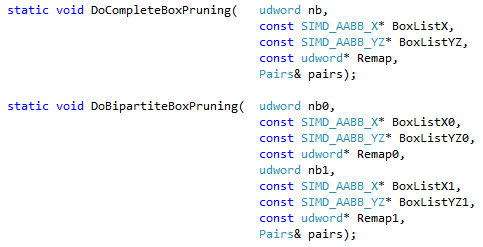
Do you remember part 1, where I mentioned the BipartiteBoxPruning function? This is the companion to the CompleteBoxPruning function we have been optimizing so far. CompleteBoxPruning finds overlaps within a set of objects. BipartiteBoxPruning finds overlap between two separate sets of objects. As we mentioned in part 1, all the optimizations we have been doing up to this point are equally valid for the bipartite case. And while I did not put any emphasis on it, I kept updating the bipartite case as well along the way.

That was by design. I knew I was going to need it eventually.

It turns out that we can take advantage of the bipartite case now, to optimize the complete case. The trick is simply to run 4 CompleteBoxPruning calls for the 4 natural buckets (as in MBP), and then run 5 additional calls:

• 1 CompleteBoxPruning call to find overlaps within the 5th bucket
• 4 BipartiteBoxPruning calls to find overlaps between the 5th bucket and buckets 1 to 4

Because of the extra calls it might be less efficient than the MBP approach overall (I did not actually try both here), but this new alternative implementation has two advantages over MBP:

• There is no need to duplicate the objects. We can simply reshuffle the same input arrays into 5 sections, without the need to allocate more memory.
• There is no need for a hash-map. This approach does not generate duplicate pairs so we can keep adding our colliding pairs to our simple dynamic array like before.

Overall this approach is much simpler to test in the context of our box-pruning project, so that is why I selected it.

Implementation in our project

First, we allocate a little bit more space than before for our split boxes. Recall that in version 16 we did something like this:

The +1 in the BoxListX allocation was initially added in version 4, to make space for a sentinel value. The extra +5 was added later when we unrolled the loops that many times. And then the +1 in BoxListYZ is actually unnecessary: it appeared when we split the boxes in version 9c (we allocated the same amount of “X” and “YZ” parts), but we only need sentinels in the X buffer so we could allocate one less element in the YZ buffer.

Now, for version 17 we are going to create 5 distinct sections within these buffers (one for each bucket). Each bucket will be processed like our arrays from version 16, i.e. each of them needs to have sentinel values. Thus for 5 buckets we need to allocate 5 times more sentinels than before, i.e. a total of 30 extra entries in the X buffer. The YZ buffer does not need extra space however, thanks to our previous observation that allocating one extra entry there was in fact not needed. The resulting code looks like this:

—

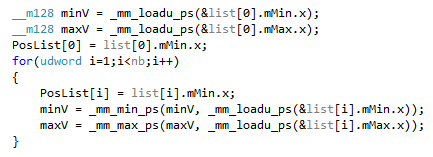
Next, we compute the initial bounding box (AABB) around the objects. This is the black bounding box in picture 1). We already had a loop over the source data to compute “PosList” in version 16, so computing an extra bounding box at the same time is cheap (it does not introduce new cache misses or new branches):

The only subtle issue here is that the last SIMD load on the last box reads 4 bytes past the end of the source array. This can crash if the last allocated entry was exactly at the end of a memory page. The simplest way to address this is to allocate one more dummy box in the source array.

—

Once the AABB is computed, we can subdivide it as shown in picture 2). We are not doing any clever analysis to find the split points: we just take the middle of the box along Y and Z. The main box-pruning code projects the boxes on the X axis already (hardcoded in Part 5), so we ignore the X axis for our broadphase regions, and we split along the two other axes:

—

These two limit values and the initial bounding box implicitly define the 4 bounding boxes around the natural buckets. With this knowledge we can then classify boxes, and assign each of them to a bucket. Because we ignore the X axis, we effectively deal with 2D boxes here. A box fully contained within one of the 4 natural buckets is given an ID between 0 and 3. A box crossing a bucket’s boundary ends up in the cross bucket, with ID 4.

The classification is a fairly straightforward matter:

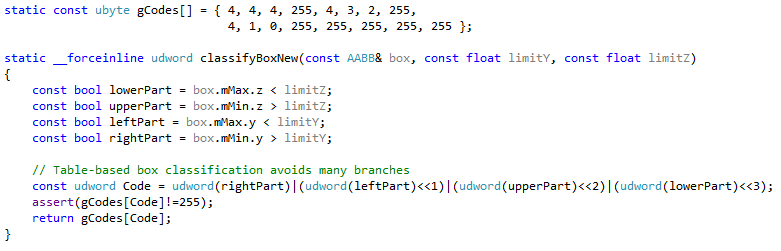
Each box is tested against the previously computed limits. In sake of completeness, let’s reverse-engineer the code. Let’s call B the main black box from Picture 1).

We see from the way it is computed that limitY is B’s center value on axis Y. We then compare it to the incoming box’s min and max Y values. We compare Y values together, that is consistent and good. If leftPart is true, it means the incoming box is fully on the left side of the split, i.e. the box does not cross the Y boundary. But if rightPart is true, the box is fully on the right side of the split. It should not be possible for leftPart and rightPart to be both true at the same time.

Similarly, limitZ is B’s center value on axis Z. We compare it to the incoming box’s min and max Z values, which is also consistent and correct. If lowerPart is true, it means the incoming box is fully on the lower side of the split, i.e. the box does not cross the Z boundary. But if upperPart is true, the box is fully on the upper side of the split. It should not be possible for lowerPart and upperPart to be both true at the same time.

The classification is then:

• leftPart && lowerPart => the box is fully in region A
• leftPart && upperPart => the box is fully in region B
• rightPart && lowerPart => the box is fully in region C
• rightPart && upperPart => the box is fully in region D

In any other case, the box is crossing at least one boundary, and thus ends up in region E – the cross bucket. Doing these comparisons is a bit costly so instead we compute a 4-bit mask from the test results and use it as an index into a small look-up table. The disassembly shows that using a table avoids branches (this is similar to what we covered in version 8):

00AE3B90 movss xmm0,dword ptr [edx]
00AE3B94 xor ecx,ecx
00AE3B96 comiss xmm2,dword ptr [edx+0Ch]
00AE3B9A lea edx,[edx+18h]
00AE3B9D seta cl
00AE3BA0 xor eax,eax
00AE3BA2 lea esi,[esi+4]
00AE3BA5 add ecx,ecx
00AE3BA7 comiss xmm0,xmm2
00AE3BAA movss xmm0,dword ptr [edx-1Ch]
00AE3BAF seta al
00AE3BB2 or ecx,eax
00AE3BB4 xor eax,eax
00AE3BB6 add ecx,ecx
00AE3BB8 comiss xmm1,dword ptr [edx-10h]
00AE3BBC seta al
00AE3BBF or ecx,eax
00AE3BC1 xor eax,eax
00AE3BC3 add ecx,ecx
00AE3BC5 comiss xmm0,xmm1
00AE3BC8 seta al
00AE3BCB or ecx,eax
00AE3BCD movzx eax,byte ptr [ecx+0B04250h]
00AE3BD4 mov dword ptr [esi-4],eax
00AE3BD7 inc dword ptr [esp+eax*4+0A0h]
00AE3BDE dec edi
00AE3BDF jne CompleteBoxPruning+1B0h (0AE3B90h)

It may not be optimal but it is good enough for now. The table is simple enough to derive. We organize the mask like this:

lowerPart | upperPart | leftPart | rightPart

Thus we get:

• 0000 - region E
• 0001 - region E
• 0010 - region E
• 0011 - leftPart/rightPart both set, not possible
• 0100 - region E
• 0101 - upperPart && rightPart => region D
• 0110 - upperPart && leftPart => region B
• 0111 - leftPart/rightPart both set, not possible
• 1000 - region E
• 1001 - lowerPart && rightPart => region C
• 1010 - lowerPart && leftPart => region A
• 1011 - leftPart/rightPart both set, not possible
• 1100 - lowerPart/upperPart both set, not possible
• 1101 - lowerPart/upperPart both set, not possible
• 1110 - lowerPart/upperPart both set, not possible
• 1111 - leftPart/rightPart both set, not possible

—

Once the bucket indices are available for all boxes, BoxXListBuffer and BoxListYZBuffer are filled with sorted boxes, like we did in version 16. The only difference is that boxes are stored per bucket there: all boxes of bucket 0 (sorted along X), then all boxes of bucket 1 (sorted along X), and so on. This part is just simple pointer and counter book-keeping, no major issue. Just remember to write all the necessary sentinels at the end of each section within the array.

—

At this point the data is ready and we can do the actual pruning. In version 16, we only had one “complete box pruning” function running there. In version 17 we will need to run multiple “complete box pruning” calls on 5 distinct parts of the arrays, and additional “bipartite box pruning” calls. Thus we first copy the corresponding code into separate functions:

This is the same code otherwise as in version 16; we just move it to separate functions.

—

Finally, we do the sequence of complete and bipartite pruning calls that we mentioned in a previous paragraph:

In these two for loops, i is the bucket index. We first find overlaps within each of the 5 buckets (the first for loop), then we find overlaps between bucket 4 (the cross bucket) and the 4 first natural buckets.

That’s it.

As promised, the modifications we made to try this new approach are somewhat minimal. There is no need to introduce a hash-map or more complicated memory management, it’s all rather simple.

Admittedly, the approach does not guarantee performance gains compared to version 16. We could very well find degenerate cases where all objects end up in the same bucket. But even in these bad cases we would effectively end up with the same as version 16, with a modest overhead introduced by the bounding box computation and box classification. Not the end of the world. Most of the time objects are distributed fairly homogeneously and the approach gives clear performance gains.

It certainly does in our test project, in any case:

What do we get?

We see clear gains compared to our previous version 16 on all machines. This is the only “apples-to-apples” comparison we have here, since the pruning code is effectively the same in both versions. So we only measure the effect of our high-level optimization here, and we can conclude that it does work.

Perhaps more interestingly, version 17 is also faster than version 15b on all tested machines. That is, our C++ SSE2 version is now faster than our best assembly SSE2 version. This is pretty good because it was the opposite before: version 15b was faster than version 16 on all machines. Of course the comparison is a bit unfair here, and we could port the high-level optimization to version 15b to get some gains there as well. However we would need to write the whole bipartite function in assembly, so that is a lot more work than what we did for the C++ version. Exercise left to the readers and all that (or to cough Fabian cough :)).

Finally, on machines that support it, the AVX version remains the fastest. Or so it seems.

The trap of the unique benchmark

In this series we have consistently made one cardinal mistake. Something that experienced programmers know is a very bad idea. We ignored the first rule of optimization 101:

Use more than one benchmark.

You need to start somewhere of course, and we’ve gone a long way with our unique test scenario in this project – so a single benchmark does provide value, and it is certainly better than no benchmark at all.

However, using a single benchmark has its perils. By nature it tends to test a single codepath, a single configuration, a single way to navigate through your code. And of course, there is absolutely no guarantee that a different scenario produces the same performance profile. There is no guarantee that a specific optimization helps in all cases. Change the input data, and maybe you reach a different conclusion. Maybe your algorithm does not scale. Maybe something helps for a large number of objects, but hurts for a small number of them. Maybe one optimization helps when a lot of boxes do overlap, but hurts when the same boxes are disjoint. And so on. There is a huge amount of combinations, codepaths, configurations, which are as many traps one can fall into.

And thus, at some point one must start using more than one benchmark. In PhysX for example, I remember creating 4 or 5 different benchmarks just to test a single box-vs-triangle overlap function (similar to my blog post here). The function had multiple codepaths, some with early exits, and I created a separate benchmark for each of them. This is impossible to do for a full physics engine, but that is the spirit.

Now this is a toy project here so I will not go crazy with the number of scenarios we support: I will just add one more, to prove a point.

Go back to the main source file where we define the test. Find this line:

const udword NbBoxes = 10000;

Then just add a zero:

const udword NbBoxes = 100000;

What happens when we test ten times more boxes?

Well the first thing one notices is that our initial versions become insufferably slow. The code now finds and reports 1144045 pairs and it brings our first versions to their knees. It is so bad that our profiling function cannot even measure the time properly: our naïve version only returned the lower 32bit part of the TSC counter (which is a 64bit value), and the initial code is so slow that we wrap around, producing meaningless timings.

So I will just ignore the first versions and show the results for latest ones. This is now for 100000 boxes:

While the timings generally follow the same pattern as in our previous test with less boxes, we clearly see that version 17 is now the fastest on all tested machines. The high-level optimization was more effective for a large number of boxes than it was for a “small” number of them.

I did not do a thorough analysis to explain why but generally speaking it is true that simple brute-force versions can be faster than smarter versions when you only have a small amount of items to process. In our case we added some overhead to compute the initial bounding box and classify boxes into buckets, which is an O(n) part, while the following pruning loops are not O(n) (as you can see with the timings: we multiplied the amount of boxes by 10 but the time it takes to process them grew by more than 10). The relative cost of the “preparation” part compared to the “pruning” part has an impact on which version is eventually the fastest.

And then again, there are different codepaths within the pruning part itself (how many overlap tests do we end up with? How many of them report a hit?) and increasing the amount of boxes might add some pressure on a codepath that was previously less traveled.

In short: one benchmark is not enough.

The bipartite case

We mentioned that until now, all our improvements to the complete case were equally valid for the bipartite case. But the optimizations for the bipartite case will be slightly different in this version, since we cannot exactly replicate there what we did for the complete case.

What we can do is the following:

• Compute buckets for both incoming sets of objects A and B (similar to what we did before)
• Compute buckets’ bounds (this is new, we did not need them in the complete case)
• Do a bipartite box pruning call between each bucket of A and each bucket of B, if their respective bounds overlap.

And with this, we can wrap this part up.

What we learnt:

Low-level optimizations are important but not the only thing to care about. High-level algorithmic optimizations are equally important.

One benchmark is not enough. Some optimizations might work in some scenarios, while being detrimental in others. Use multiple benchmarks with various workloads and various configurations, to stress multiple codepaths.

We can make the complete-box-pruning codepath faster using the bipartite-box-pruning codepath. But we cannot make the bipartite case faster using the complete case. For the first time the bipartite case needed specific changes.

We reached our goal of being faster than the AVX version, at least in some scenarios.

So… are we finally done?

Ah.

Not really.

We just opened the door to high-level optimizations, so we still have a long way to go.

GitHub code for version 17 is here.

I never announced it here but I’m on Twitter. I post there a lot more than I post here

Part 16 – improved pair reporting

In Part 15 we saw that there were some cycles to save in the part of the code that reports pairs.

By nature, the AVX version had to report multiple results at the same time. Thus in this context it was natural to end up modifying the part that reports overlaps.

But there was no incentive for me to touch this before, because that part of the code is not something that would survive as-is in a production version. In the real world (e.g. in an actual physics engine), the part reporting overlapping pairs tends to be more complicated (and much slower) anyway. In some cases, you need to output results to a hash-map instead of just a dynamic vector. In some cases, you need to do more complex filtering before accepting a pair. Sometimes that means going through a user-defined callback to let customers apply their own logic and decide whether they want the pair or not. All these things are much slower than our simple pair reporting, so basically this is not the place we should bother optimizing.

That being said, the code reporting overlaps does have obvious issues and in the context of this project it is certainly fair game to address them. So, let’s revisit this now.

So far we have used a simple container class to report our pairs, which was basically equivalent to an std::vector<int>. (If you wonder why I didn’t use an actual std::vector, please go read Part 11 again).

The code for adding an int to the container (equivalent to a simple push_back) was:

And the code to add a pair to the array was something like:

So there are two obvious issues here:

• Because we add the two integers making up a pair separately, we do two resize checks (two comparisons) per pair instead of one. Now the way the benchmark is setup, we resize the array during the first run, but never again afterwards. So in all subsequent runs we always take the same branch, and in theory there shouldn’t be any misprediction. But still, that’s one more comparison & jump than necessary.
• We update mCurNbEntries twice per pair instead of one. Since this is a class member, this is exactly the kind of things that would have given a bad load-hit-store (LHS) on Xbox 360. I did not investigate to see what kind of penalty (if any) it produced on PC in this case, but regardless: we can do better.

I am aware that none of these issues would have appeared if we would have used a standard std::vector<Pair> for example. However, we would have had other issues - as seen in a previous report. I used this non-templated custom array class in the original code simply because this is the only one I was familiar with back in 2002 (and the class itself was older than that, records show it was written around February 2000. Things were different back then).

In any case, we can address these problems in a number of ways. I just picked an easy one, and I now create a small wrapper passed to the collision code:

And the pairs are now reported as you’d expect from reading the code:

So it just does one comparison and one class member read-modify-write operation per pair, instead of two. Trivial stuff, there isn’t much to it.

But this simple change is enough to produce measurable gains, reported in the following tables. Version16 there should be compared to Version 14d – it’s the same code, only the pair reporting function has changed.

(*) There was an error for this number in Part 15. It said “13.79” instead of “13.37” like in previous reports.

The gains are all over the place: 561 K-Cycles on one machine, 268 K-Cycles on another and a disappointing 155 K-Cycles on my home desktop PC. That last one rings a bell: I have a vague memory of removing the entire pair report mechanism at some point on this PC, to check how much the whole thing was costing me. The gains were so minimal I didn’t bother investigating further.

For some reason the new machines give better gains. Due to lack of time (and lack of motivation: this part of the code is not very interesting to me), I did not investigate why. It’s faster for “obvious” theoretical reasons (we do less work), we see gains in practice (at least we don’t get slower results), that’s good enough for now.

Similarly there would be more to do to fully replicate Ryg’s changes from the AVX version. By nature the AVX version reports multiple pairs at the same time, but in a way the same can be said about our unrolled loops, and we could try to use the same strategies there. For example the resize check could be done only once before a loop unrolled N times starts, making sure that there is enough space in the array to write N pairs there (without extra checks). But I did not bother investigating further at this point: I am happy with the gains we got from the trivial change, and if the AVX version still has a small additional advantage from its improved pair reporting code, so be it.

What we learnt:

The “C++” code I wrote 15 years ago was not great. That pair reporting part was a bit lame. But then again 15 years ago I had never heard of load-hit-store penalties.

Show your code. Put it online. People will pick it up and point out the issues you forgot or didn’t know you had in there.

We closed the gap a bit between our best “C++” SSE2 version and the fastest available SSE2 assembly version.

This was probably the last “easy” optimization available before tackling something much bigger.

GitHub code for version 16 is here.

Part 15 – AVX

In version 14b we looked at Ryg’s initial experiments with this project. If you followed his progress on GitHub, you probably already know that he went ahead and did a lot more than what we covered so far. In particular, his latest version uses AVX instructions. I couldn’t try this myself before, since my PC did not support them. But things are different now (see previous post) so it’s time to look at Ryg’s most recent efforts (which are already one year old at this point).

According to Steam’s hardware survey from April 2018, AVX is widely available (86%) but still not as ubiquitous as SSE2 (100%!):

That’s why I never really looked at it seriously so far. At the end of the day, and in the back of my mind, I would like to use these optimizations on PC but also other platforms like consoles. Hopefully we will go back to this later in the series - I did run all these tests on consoles as well, and the results are not always the same as for the PC. In PhysX we are already suffering from the power difference between a modern PC and current-gen consoles: the consoles are sometimes struggling to handle something that runs just fine on PC. Using AVX would only tip the scales even more in favor of PCs. That being said, we had the same discussion about SSE2 back in the days, and now SSE2 is everywhere… including on consoles. So it is reasonable to expect AVX to be available in all next-gen consoles as well, and the time spent learning it now is hopefully just a good investment for the future. (I would totally take that time and play with AVX just for fun if I wouldn’t have a child. But these days my free time is severely limited, as you noticed with the one year gap between 14d and 14e, so I have to choose my targets wisely).

Alright.

Like last time, Fabian was kind enough to include detailed notes about what he did. So, I will just copy-paste here what you probably already read a year ago anyway. In his own words:

Here’s what I did to the code to arrive at the current version:

I already wrote a note on the earlier changes that were just cleaning up the ASM code and unrolling it a bit. That text file is a gist and available here:

https://gist.github.com/rygorous/fdd41f45b24472649aaeb5b55bbe6e26

…and then someone on Twitter asked “what if you used AVX instead of SSE2?”. My initial response boiled down to “that’s not gonna work with how the loop is currently set up”. The problem is that the original idea of having one box=4 floats, doing all 4 compares with a single SSE compare, doing a movemask, and then checking whether we get the number that means “box intersects” (12 in the original case) fundamentally doesn’t translate well to 8-wide: now instead of one box per compare, we’re testing two (let’s call them box1[0] and box1[1]), and instead of two possible outcomes, we now have four, where ? stands for any hex digit but ‘c’:

1. Both box1[0] and box1[1] intersect box0. (=movemask gives 0xcc)
2. box1[0] intersects box0, box1[1] doesn’t. (=movemask gives 0x?c)
3. box1[1] intersects box0, box1[0] doesn’t. (=movemask gives 0xc?)
4. neither intersects box0. (=movemask gives 0x??)
   

Instead of the previous solution where we had exactly one value to compare against, now we need to do a more expensive test like “(mask & 0xf) == 12 || (mask & 0xf0) == 0xc0″. Not the end of the world, but it means something like

mov tmp, eax
and tmp, 15
cmp tmp, 12
je  FoundOne
and eax, 15
cmp eax, 12
je  FoundOne

which is one more temp register required and several extra uops, and as we saw in the gist, this loop was pretty tight before. Whenever something like this happens, it’s a sign that you’re working against the grain of the hardware and you should maybe take a step back and consider something different.

That “something different” in this case was converting the loop to use a SoA layout (structure of arrays, google it, enough has been written about it elsewhere) and doing some back of the envelope math (also in this repository, “notes_avx.txt”) to figure out how much work that would be per loop iteration. End result: 12 fused uops per iter to process *8* boxes (instead of 20 fused uops/iter to process 4 using SSE2!), still with a fairly decent load balance across the ports. This could be a win, and not just for AVX, but with SSE2 as well.

Addressing
———-

The first problem was that this code is 32-bit x86, which is register-starved, and going to SoA means we (in theory) need to keep around five pointers in the main loop, instead of just one.

Possible (barely) but very inconvenient, and there’s no way you want to be incrementing all of them. Luckily, we don’t have to: the first observation is that all the arrays we advance through have the same element stride (four bytes), so we don’t actually need to keep incrementing 5 pointers, because the distances between the pointers always stay the same. We can just compute those distances, increment *one* of the pointers, and use [reg1+reg2] addressing modes to compute the rest on the fly.

The second trick is to use x86’s scaling indexing addressing modes: we can not just use address expressions [reg1+reg2], but also [reg1+reg2*2], [reg1+reg2*4] and [reg1+reg2*8] (left-shifts by 0 through 3). The *8 version is not very useful to use unless we want to add a lot of padding since we’re just dealing with 6 arrays, but that narrows us down to four choices:

1. [base_ptr]
2. [base_ptr + dist]
3. [base_ptr + dist*2]
4. [base_ptr + dist*4]

and we need to address five arrays in the main loop. So spending only 2 registers isn’t really practical unless we want to allocate a bunch of extra memory. I opted against it, and choose 2 “dist” registers, one being the negation of the other. That means we can use the following:

1. [base_ptr]
2. [base_ptr + dist_pos]
3. [base_ptr + dist_pos*2]
4. [base_ptr - dist_pos] = [base_ptr + dist_neg]
5. [base_ptr - dist_pos*2] = [base_ptr + dist_neg*2]

ta-daa, five pointers in three registers with only one increment per loop iteration. The layout I chose arranges the arrays as follows:

1. BoxMaxX[size]
2. BoxMinX[size]
3. BoxMaxY[size]
4. BoxMinY[size]
5. BoxMaxZ[size]
6. BoxMinZ[size]

which has the 5 arrays we keep hitting in the main loop all contiguous, and then makes base_ptr point at the fourth one (BoxMinY).

You can see this all in the C++ code already, although it really doesn’t generate great code there. The pointer-casting to do bytewise additions and subtractions is all wrapped into “PtrAddBytes” to de-noise the C++ code. (Otherwise, you wouldn’t able to see anything for the constant type casts.)

Reporting intersections (first version)
—————————————

This version, unlike Pierre’s original approach, “natively” processes multiple boxes at the same time, and only does one compare for the bunch of them.

In fact, the basic version of this approach is pretty canonical and would be easily written in something like ISPC (ispc.github.io). Since the goal of this particular version was to be as fast as possible, I didn’t do that here though, since I wanted the option to do weird abstraction-breaking stuff when I wanted to.

Anyway, the problem is that now, we can find multiple pairs at once, and we need to handle this correctly.

Commit id 9e171cf6 has the basic approach: our new ReportIntersections gets a bit mask of reported intersections, and adds the pairs once by one. This loop uses an x86 bit scan instruction (”bsf”) to find the location of the first set bit in the mask, remaps its ID, then adds it to the result array, and finally uses “mask &= mask - 1;” which is a standard bit trick to clear the lowest set bit in a value.

This was good enough at the start, although I later switched to something else.

The basic loop (SSE version)
—————————-

I first started with the SSE variant (since the estimate said that should be faster as well) before trying to get AVX to run. Commit id 1fd8579c has the initial implementation. The main loop is pretty much like described in notes_avx.txt (edi is our base_ptr, edx=dist_neg, ecx=dist_pos).

In addition to this main loop, we also need code to process the tail of the array, when some of the boxes have a mMinX > MaxLimit. This logic is fairly easy: identify such boxes (it’s just another compare, integer this time since we convertred the MinX array to ints) and exclude them from the test (that’s the extra “andnps” - it excludes the boxes with mMinX > MaxLimit). This one is sligthly annoying because SSE2 has no unsigned integer compares, only signed, and my initial “MungeFloat” function produced unsigned integers. I fixed it up to produce signed integers that are currently ordered in an earlier commit (id 95eaaaac).

This version also needs to convert boxes to SoA layout in the first place, which in this version is just done in straight scalar C++ code.

Note that in this version, we’re doing unaligned loads from the box arrays. That’s because our loop counters point at an arbitrary box ID and we’re going over boxes one by one. This is not ideal but not a showstopper in the SSE version; however, it posed major problems for…

The AVX version
—————

As I wrote in “notes_avx.txt” before I started, “if the cache can keep up (doubt it!)”. Turns out that on the (Sandy Bridge) i7-2600K I’m writing this on, writing AVX code is a great way to run into L1 cache bandwidth limits.

The basic problem is that Sandy Bridge has full 256-bit AVX execution, but “only” 128-bit wide load/store units (two loads and one store per cycle). A aligned 256-bit access keeps the respective unit busy for 2 cycles, unaligned 256b accesses are three (best case).

In short, if you’re using 256-bit vectors on SNB, it’s quite easy to swamp the L1 cache with requests, and that’s what we end up doing.

The initial AVX version worked, but ended up being slightly slower than the (new) SSE2 version. Not very useful.

To make it competitive, it needed to switch to aligned memory operations. Luckily, in this case, it turns out to be fairly easy: we just make sure to allocate the initial array 32-byte aligned (and make sure the distance between arrays is a multiple of 32 bytes as well, to make sure that if one of the pointers is aligned, they all are), and then make sure to get us to a 32-byte aligned address before we enter the main loop.

So that’s what the first real AVX version (commit 19146649) did. I found it a bit simpler to round the current box pointer *down* to a multiple of 32, not up. This makes the first few lanes garbage if we weren’t already 32-byte aligned; we can deal with this by masking them out, the same way we handled the mMinX > MaxLimit lanes in the tail code.

And with the alignment taken care of, the AVX version was now at 3700 Kcycles for the test on my home machine, compared to about 6200 Kcycles for the SSE2 version! Success.

Cleaning up the setup
———————

At this point, the setup code is starting to be a noticeable part of the overall time, and in particular the code to transform the box array from AoS to SoA was kind of ratty. However, transforming from AoS to SoA is a bog-standard problem and boils down to using 4×4 matrix transposition in this case. So I wrote the code to do it using SIMD instructions instead of scalar too, for about another 200 Kcycles savings (in both the AVX and SSE2 vers).

Reporting intersections (second version)
—————————————-

After that, I decided to take a look with VTune and discovered that the AVX version was spending about 10% of its time in ReportIntersections, and accruing pretty significant branch mis-prediction penalties along the way.

So, time to make it less branchy.

As a first step, added some code so that instead of writing to “Container& pairs” directly, I get to amortize the work. In particular, I want to only do the “is there enough space left” check *once* per group of (up to) 8 pairs, and grow the container if necessary to make sure that we can insert those 16 pairs without further checks. That’s what “PairOutputBuffer” is for. It basically grabs the storage from the given Container while it’s in scope, maintains our (somewhat looser) invariants, and is written for client code that just wants to poke around in the pointers directly, so there’s no data hiding here. That was finalized in commit 389bf503, and decreases the cost of ReportIntersections slightly.

Next, we switch to outputting the intersections all at once, using SIMD code. This boils down to only storing the vector lanes that have their corresponding mask bit set. This is a completely standard technique. Nicely enough, Andreas Frediksson has written it up so I don’t have to:

https://deplinenoise.files.wordpress.com/2015/03/gdc2015_afredriksson_simd.pdf

(The filter/”left packing” stuff). AVX only exists on machines that also have PSHUFB and POPCNT so we can use both.

This indeed reduced our CPU time by another ~250 Kcycles, putting the AVX version at about 3250 Kcycles! And that’s where it currently still is on this machine. (That version was finalized in commit id f0ca3dc1).

Porting back improvements to SSE2/Intrinsics code
————————————————-

Finally, I decided to port back some of these changes to the SSE2 code and the C++ intrinsics version. In particular, port the alignment trick from AVX to SSE2 for a very significant win in commit d92dd5f9, and use the SSE2 version of the left-packing trick in commit 69baa1f1 (I could’ve used SSSE3 there, but I didn’t want to gratuitously increase the required SSE version).

And then I later ported the left-packing trick for output to the C++ intrinsics version as well. (The alignment trick does not help in the intrinsics ver, since the compiler is not as good about managing registers and starts tripping all over its feet when you do it.)

Thank you Ryg.

That is quite a lot of stuff to digest. I guess we can first look at the results on my machines. There are 3 different versions in Fabian’s last submits:

• an SSE2 version using intrinsics
• an SSE2 version using assembly
• an AVX version using assembly

And I now have 3 different PCs available: my old home desktop PC (one of the two used in the initial posts for this serie, the other one died), a new office desktop PC, and a new home laptop PC. So that’s 9 results to report. Here they are (new entries in bold):

So first, we see that the performance of the SSE2 intrinsics version is quite different depending on where you run it. It is fine on my more recent machines, but it is quite bad on my older home desktop PC, where it is roughly similar to version 9c in terms of speed. That is a clear regression compared to our latest unrolled versions. I did not investigate what the problem could be, because even on modern PCs the performance is ultimately not as good as our best “version 14″. On the other hand, this version (let’s call it 15a) is not as ugly-looking as 14c or 14d. So provided we could fix its performance issue on the home desktop PC, it could be an interesting alternative which would remain somewhat portable.

Then, we have version 15b. This one is pretty good and offers a clear speedup over our previous SSE2 versions. This is interesting because it shows that without going all the way to AVX (i.e. without losing compatibility with some machines), the AVX “philosophy” if you want (re-organizing the code to be AVX-friendly) still has some potential performance gains. Ideally, we would be able to get these benefits in the C++ code as well. Admittedly this may not be easy since this is essentially what 15a failed to do, but we might be able to try again and come up with a better 15a implementation. Somehow.

Finally, version 15c is the actual AVX version. Unsurprisingly if I bypass the AVX check and run it on my home desktop PC, it crashes - since that PC does not support AVX. On the other hand, on the machines that do support it, performance is awesome: we get pretty much the advertised 2X speedup over regular SIMD that AVX was supposed to deliver. And thus, with this, we are now about 24X to 27X faster than the original code. Think about that next time somebody claims that low-level optimizations are not worth it anymore, and that people should instead focus on multi-threading the code: you would need a 24-core processor and perfect scaling to reach an equivalent speedup with multi-threading…

So, where do we go from here?

I had plans for where to move this project next, but now a whole bunch of new questions arose.

Some of these optimizations like the one done for reporting intersections in a less branchy way seem orthogonal to AVX, and could potentially benefit our previous versions as well. The way these AVX versions have been delivered, combining multiple new optimizations into the same new build, it is slightly unclear how much the performance changed with each step (although Ryg’s notes do give us a clue). I usually prefer doing one optimization at a time (each in separate builds) to make things clearer. In any case, we could try to port the improved code for reporting intersections to version 14 and see what happens.

Fabian initially claimed that the design did not translate well to 8-wide, and thus we had to switch to SoA. I didn’t give it much thoughts but I am not sure about this yet. I think the dismissed non-existing version where we would test 2 boxes at a time with AVX could still give us some gains. The movemask test becomes slightly more expensive, yes, but we still drop half of the loading+compare+movemask instructions. That must count for something? Maybe I am being naive here.

Another thing to try would be to dive into the disassembly of version 15a, figure out why it performs badly on the home desktop PC, and fix it / improve it. That could be a worthwhile goal because I really didn’t want to move further into assembly land. Quite the opposite: one of the planned next posts was about checking the effects of these optimizations on ARM and different architectures. Assembly versions are a show-stopper there - we cannot even have inline assembly on Win64 these days. So at the very least versions 15b and 15c give us new targets and show us what is possible in terms of performance. But I will have difficulties keeping them around for long.

And this brings us to the obvious question about 15c: could we try it using AVX intrinsics instead of assembly? That could be a way to keep some portability (at least between Win32 and Win64) while still giving us some of the AVX performance gains.

Another thing that comes to mind is that we saw in part 3 that the sorting was costing us at best 140 K-Cycles (and in reality, much more). This was negligible at the time, but Ryg’s latest optimizations were about saving ~200 K-Cycles, so this part is becoming relevant again. One strategy here, if we don’t want to deal with this just yet, could be to reset the test and use more boxes. We used 10000 boxes so far, but we could just add a 0 there and continue our journey.

Beyond that, I had further optimizations planned for the whole project, which are completely orthogonal to AVX. So I could just continue with that and ignore the AVX versions for now. A new goal could be for me to reach the same performance as the AVX assembly version, but using another way, with regular SSE intrinsics.

Here is a potential TODO list for further reports:

1. Try the optimized intersections report in version 14.
2. Try an AVX version that tests 2 boxes at a time without SoA.
3. Analyze the 15a disassembly and try to fix it (make it fast on my home desktop PC).
4. Try a version using AVX intrinsics.
5. Revisit the sorting code (and general setup code) in version 14/15.
6. Go ahead with the initial plan and further non-AVX-related optimizations (that’s at least 3 more blog posts there).
7. Once it’s done, merge AVX optimizations to these new versions for further speedup.
8. When applicable, check the performance of all these versions on other platforms / architecture. That’s when having a separate build per optimization pays off: do we have some optimizations that hurt instead of help on some platforms?
9. Investigate how the performance varies and which version is the fastest when the number of objects changes.
10. Explain what it takes to productize this and make it useful in a real physics engine (in particular: how you deal with sleeping objects and how you report new and deleted pairs instead of all of them).
11. Field test.

I don’t know yet what I will try next, or when, but it seems that there is indeed, more than ever, still a lot to do.

What we learnt:

AVX works. It does not happen every day but it can make your code 2X faster than regular SSE.

You might need assembly for that to happen though. Like it or not, assembly wins again today.

Do not ignore low level optimizations. In our case there was a 24X performance gain on the table (so far), without changing the algorithm, without multi-threading. Typical multi-threading will give you much less than that.

GitHub code for version 15 is here.

I apologize for the lack of new material, it is really just the same as what Fabian published a year ago. I did a minor modification to be able to run the SSE2 versions on AVX-enabled machines, so you now have to select the desired version with a define in the code.

Part 14e – a bugfix and a reboot

More than a year after version 14d, I finally come back to this project for a brief update.

So, basically, a year ago my office PC died, and it rendered half of the published timings obsolete and irrelevant. I got a replacement PC, with a more recent CPU and different features (AVX in particular). I thought I would pause the project for maybe a month (a lot of things ended up on my plate at work), but before I knew it a year had disappeared.

Oh well. That’s life. Especially when you have kids.

—

Another thing that happened is that I found a bug in version 14d. The code computing the box index in the bipartite case was wrong (off by one error). Since I had no validity test for the bipartite case, and because the reported number of pairs was correct, I did not notice that one for a while.

Right. So here is version 14e, which is pretty much the same as version 14d except:

• The bug has been fixed.
• A validity test for the bipartite case has been added.
• The bipartite case has been refactored to avoid duplicating the loop.

The bugfix has no impact on performance. We only tracked the performance of the “complete box pruning” codepath anyway.

What does have an impact on performance though, is the new PC. I had no choice but re-measure all versions on this new machine. The results are listed in Table 1.

While I was at it, I ran the same tests on my wife’s laptop at home. I should have tried that sooner: turns out her laptop is more advanced than my desktop PC – it has AVX, and it is much faster! The results for that laptop are listed in Table 2.

We only keep what we previously called “safe” versions now. We do not list the timings for the “unsafe” versions anymore. I also dropped the Delta and Speedup columns to make things easier.

Table 1 – results for new office desktop PC

Table 2 – results for home laptop

We can see that the new machines are faster overall than the ones we used before, but overall the results are pretty similar to what we previously saw.

What we learnt:

A bug can remain invisible for a year, even when the code is public on GitHub. I guess nobody tried to use it.

Time passes way too quickly.

We are back on track.

GitHub code for part 14e

Quick little experiment on GitHub:

https://github.com/Pierre-Terdiman/RadixRedux

Related small article is here.

I’m afraid I don’t have a lot of time these days.

Here.

Part 14d – integer comparisons redux

In this part, we complete the port of Fabian Giesen’s code (version 14b) to C++.

In part 7 we replaced float comparisons with integer comparisons (a very old trick), but dismissed the results because the gains were too small to justify the increase in code complexity. However we made the code significantly faster since then, so the relatively small gains we got at the time might be more interesting today.

Moreover, Fabian’s version uses integers for the X’s values only. This may also be a more interesting strategy than using them for everything, like in version 7.

Let’s try!

Replicating this in the C++ version is trivial. Read part 7 again for the details. The only difference is that Fabian uses a different function to encode the floats:

// Munge the float bits to return produce an unsigned order-preserving
// ranking of floating-point numbers.
// (Old trick: http://stereopsis.com/radix.html FloatFlip, with a new
// spin to get rid of -0.0f)
// In /fp:precise, we can just calc “x + 0.0f” and get what we need.
// But fast math optimizes it away. Could use #pragma float_control,
// but that prohibits inlining of MungeFloat. So do this silly thing
// instead.
float g_global_this_always_zero = 0.0f;
static inline udword MungeFloat(float f)
{
union
{
float f;
udword u;
sdword s;
} u;
u.f = f + g_global_this_always_zero; // NOT a nop! Canonicalizes -0.0f to +0.0f
udword toggle = (u.s >> 31) | (1u << 31);
return u.u ^ toggle;
}

While my version from part 7 was simply:

static __forceinline udword encodeFloat(udword ir)
{
if(ir & 0×80000000) //negative?
return ~ir;//reverse sequence of negative numbers
else
return ir | 0×80000000; // flip sign
}

So it’s pretty much the same: given the same input float, the two functions return the same integer value, except for -0.0f. But that’s because Fabian’s code transforms -0.0f to +0.0f before doing the conversion to integer, it’s not a side-effect of the conversion itself.

This is not really needed, since both the sorting code and the pruning code can deal with -0.0f just fine. However it is technically more correct, i.e. more in line with what float comparisons would give, since with floats a positive zero is equal to a negative zero. So it is technically more correct to map both to the same integer value – which is what Fabian’s code does.

In practice, it means that my version could produce “incorrect” results when positive and negative zeros are involved in the box coordinates. But it would only happen in edge cases where boxes exactly touch, so it would be as “incorrect” as our “unsafe” versions from past posts, and we already explained why they weren’t a big issue. Still, Fabian’s version is technically superior, even if the code does look a bit silly indeed - but in a cute kind of way.

Now a perhaps more interesting thing to note is that Fabian’s version (well, Michael Herf’s version I suppose) is branchless. So could it be measurably faster?

Without further ado, here are the results on my machines – new entries in bold letters:

Version 14d uses integer comparisons for X’s. The P variant uses Pierre’s encoding function (“encodeFloat”), while the F variant uses Fabian’s (“MungeFloat”). The deltas are computed against Version 14c this time, to measure the speedup due to integer comparisons (rather than the speedup due to loop unrolling + integer comparisons).

The first thing we see is that indeed, using integer comparisons is measurably faster. This is not a big surprise since we saw the same in Version 7. But the gains are still very small (in particular, smaller than the theoretical 6% predicted by Ryg’s analysis) and to be honest I would probably still ignore them at this point. But using integers just for X’s is easy and doesn’t come with the tedious switch to integer SIMD intrinsics, so it’s probably not a big deal to keep them in that case.

On the other hand…

For some reason “encodeFloat” is faster on my home PC, while on my office PC it’s slower (and “MungeFloat” wins). This is unfortunate and slightly annoying. This is the kind of complications that I don’t mind dealing with if the gains are important, but for such small gains it starts to be a lot of trouble for minor rewards. I suppose I could simply pick up Ryg’s version because it’s more correct, and call it a day. That gives a nicely consistent overall X factor (13.37 vs 13.34) on the two machines.

And with this, we complete the port of Fabian’s assembly version to C++. Our new goal has been reached: we’re faster than version 14b now… at least on these two machines.

What we learnt:

An optimization that didn’t provide “significant gains” in the past might be worth revisiting after all the other, larger optimizations have been applied.

Similarly, we are slowly reaching a point where small differences in the setup code become measurable and worth investigating. There might be new optimization opportunities there. For example the question we previously dismissed about what kind of sorting algorithm we should use might soon come back to the table.

In any case, for now we reached our initial goal (make the code an order of magnitude faster), and we reached our secondary goal (make the C++ code faster than Ryg’s assembly version).

Surely we’re done now!?

How much longer can we keep this going?

Well… Don’t panic, but there is still a lot to do.

Stay tuned!

GitHub code for part 14d

Part 14c – that’s how I roll

Our goal today is to look at the details of what Fabian “Ryg” Giesen did in version 14b (an assembly version), and replicate them in our C++ unrolled version (14a) if possible.

First, let’s get one thing out of the way: I will not switch back to integer comparisons in this post. I like to do one optimization at a time, as you can probably tell by now, so I will leave this stuff for later. This means we can ignore the MungeFloat function and the integer-related changes in Fabian’s code.

Then, the first thing you can see is that the code has been separated in two distinct loops: a fast one (starting with the FastLoop label), and a safe one (starting with the CarefulLoop label).

One problem when unrolling the initial loop is that we don’t know ahead of time how many iterations we will have to do (it can stop at any time depending on the value of X we read from the buffer). It is much easier to unroll loops that are executed a known number of times when the loop starts.

Sometimes in this situation, one can use what I call the “radix sort strategy”: just use two passes. Count how many iterations or items you will have to deal with in a first pass, then do a second pass taking advantage of the knowledge. That’s what a radix-sort does, creating counters and histograms in a first pass. But that kind of approach does not work well here (or at least I didn’t manage to make it work).

Fabian’s approach is to just “look ahead” and check that the buffer still has at least 4 valid entries. If it does, he uses the “fast loop”. Otherwise he falls back to the “safe loop”, which is actually just our regular non-unrolled loop from version 12. In order to look ahead safely, the sentinel values are replicated as many times as we want to unroll the loop. This is a rather simple change in the non-assembly part of the code. First there:

SIMD_AABB_X* BoxListX = new SIMD_AABB_X[nb+5];

And then there:

BoxListX[nb+1].mMinX = ~0u;
BoxListX[nb+2].mMinX = ~0u;
BoxListX[nb+3].mMinX = ~0u;
BoxListX[nb+4].mMinX = ~0u;

That’s not assembly so no problem porting this bit to the C++ version.

Now, the “fast loop” is fast for three different reasons. First, it is unrolled four times, getting rid of the corresponding branching instructions – same as in our version 14a. Second, because we looked ahead and we know the four next input values are all valid, the tests against the MaxLimit value can also be removed. And finally, the idea we wanted to test at the end of 14a has also been implemented, i.e. we don’t need to increase the Offset value for each box (we can encode that directly into the address calculation).

At the end of the day, the core loop in Fabian’s version is thus:

// Unroll 0
movaps xmm3, xmmword ptr [edx+ecx*2+0] // Box1YZ
cmpnleps xmm3, xmm2
movmskps eax, xmm3
cmp eax, 0Ch
je FoundSlot0

// Unroll 1
movaps xmm3, xmmword ptr [edx+ecx*2+16] // Box1YZ
cmpnleps xmm3, xmm2
movmskps eax, xmm3
cmp eax, 0Ch
je FoundSlot1

// Unroll 2
movaps xmm3, xmmword ptr [edx+ecx*2+32] // Box1YZ
cmpnleps xmm3, xmm2
movmskps eax, xmm3
cmp eax, 0Ch
je FoundSlot2

// Unroll 3
movaps xmm3, xmmword ptr [edx+ecx*2+48] // Box1YZ
add ecx, 32 // Advance
cmpnleps xmm3, xmm2
movmskps eax, xmm3
cmp eax, 0Ch
jne FastLoop

That is only 5 instructions per box, compared to the 8 we got in version 14a. Color-coding it reveals what happened: in the same way that we moved the green blocks out of the loop in version 14a, Fabian’s version moved the blue blocks out of the (fast) loop. There is only one surviving blue instruction, to increase our offset only once for 4 boxes.

Pretty neat.

In our C++ code it would mean that the two lines marked in bold letters would / should vanish from our BLOCK macro:

Now another difference is that since we don’t increase the offset each time, we cannot jump to the same address at each stage of the unrolled code. You can see that in Fabian’s code, which jumps to different labels (FoundSlot0, FoundSlot1, FoundSlot2, or FastFoundOne). This is easy to replicate in C++ using goto. If you don’t want to use goto, well, good luck.

And that’s pretty much it. Let’s try to replicate this in C++.

As we said, replicating the setup code is trivial (it was already done in C++).

For the safe loop, we are actually going to use our previous unrolled VERSION3 from part 14a. In that respect this is an improvement over Fabian’s code: even our safe loop is unrolled. From an implementation perspective it couldn’t be more trivial: we just leave the code from part 14a as-is, and start writing another “fast” unrolled loop just before – the fallback to the safe loop happens naturally.

Now for our fast loop, we transform the BLOCK macro as expected from the previous analysis:

As we mentioned, the lines previously marked in bold vanished. Then we added two extra parameters: one (“x”) to include the offset directly in the address calculation (as we wanted to do at the end of version 14a, and as is done Fabian’s code), and another one (“label”) to make the code jump to a different address like in the assembly version.

Now, one small improvement over Fabian’s code is that we will put the “overlap found” code before the fast loop starts, not after it ends. That’s what we did in version 14a already, and it saves one jump.

Another improvement is that we’re going to unroll 5 times instead of 4, as we did in version 14a. That’s where using BLOCK macros pays off: unrolling one more time is easy and doesn’t expand the code too much.

After all is said and done, the code becomes:

I know what you’re going to say (hell, I know what you did say after I posted a preview of part 14): it looks horrible.

Sure, sure. But once again: see through the C++, and check out the disassembly for our fast loop:

001E30B0 comiss xmm2,dword ptr [edi+esi+28h]
001E30B5 jb StartLoop4+12Fh (01E31D4h)
{
BLOCK4(0, FoundOverlap0)
001E30BB movaps xmm0,xmmword ptr [ecx-20h]
001E30BF cmpnltps xmm0,xmm1
001E30C3 movmskps eax,xmm0
001E30C6 cmp eax,0Fh
001E30C9 je StartLoop4+9Bh (01E3140h)
BLOCK4(8, FoundOverlap1)
001E30CB movaps xmm0,xmmword ptr [ecx-10h]
001E30CF cmpnltps xmm0,xmm1
001E30D3 movmskps eax,xmm0
001E30D6 cmp eax,0Fh
001E30D9 je StartLoop4+8Bh (01E3130h)
BLOCK4(16, FoundOverlap2)
001E30DB movaps xmm0,xmmword ptr [ecx]
001E30DE cmpnltps xmm0,xmm1
001E30E2 movmskps eax,xmm0
001E30E5 cmp eax,0Fh
001E30E8 je StartLoop4+7Bh (01E3120h)
BLOCK4(24, FoundOverlap3)
001E30EA movaps xmm0,xmmword ptr [ecx+10h]
001E30EE cmpnltps xmm0,xmm1
001E30F2 movmskps eax,xmm0
001E30F5 cmp eax,0Fh
001E30F8 je StartLoop4+6Dh (01E3112h)
// BLOCK4(32, FoundOverlap4)
Offset += 40;
BLOCK4(-8, FoundOverlap)
001E30FA movaps xmm0,xmmword ptr [ecx+20h]
001E30FE add ecx,50h
001E3101 cmpnltps xmm0,xmm1
001E3105 add esi,28h
001E3108 movmskps eax,xmm0
001E310B cmp eax,0Fh
001E310E jne StartLoop4+0Bh (01E30B0h)
}
001E3110 jmp StartLoop4+0ABh (01E3150h)

That’s pretty much perfect.

We get an initial comiss instruction instead of cmp because we didn’t bother switching X’s to integers, and we see the loop has been unrolled 5 times instead of 4, but other than that it’s virtually the same as Fabian’s code, which is what we wanted.

We get the following results:

The deltas in the results are compared to version 13, similar to what we did for version 14a.

Thanks to our small improvements, this new version is actually faster than version 14b (at least on my machines) – without using integers! As a bonus, this is based on the “safe” version 14a rather than the “unsafe” version 12.

What we learnt:

Once again the assembly version showed us the way. I am not sure I would have “seen” how to do this one without an assembly model I could copy.

Ugly C++ can generate pretty good looking assembly – and vice versa.

Unrolling is like SIMD: tricky. It’s easy to get gains from some basic unrolling but writing the optimal unrolled loop is quite another story.

Stay tuned. In the next post we will complete our port of Fabian’s code to C++, and revisit integer comparisons.

GitHub code for part 14c

Part 14b – Ryg rolling

After I wrote about this project on Twitter, Fabian “Ryg” Giesen picked it up and made it his own. For those who don’t know him, Fabian works for RAD Game Tools and used to be / still is a member of Farbrausch. In other words, we share the same demo-scene roots. And thus, it is probably not a surprise that he began hacking the box-pruning project after I posted version 12 (the assembly version).

Now, at the end of part 14a we thought we could still improve the unrolled code by taking advantage of the address calculation to get rid of some more instructions. As it turns out, Fabian’s code does that already.

And much more.

Since he was kind enough to write some notes about the whole thing, I will just copy-paste his own explanations here. This is based on my assembly version (i.e. box pruning version 12), and this is just his initial attempt at optimizing it. He did a lot more than this afterwards. But let’s do one thing at a time here.

In his own words:

—-

Brief explanation what I did to get the speed-up, and the thought process behind it.

The original code went:

My first suggestion was to restructure the loop slightly so the hot “no overlap” path is straight-line and the cold “found overlap” path has the extra jumps. This can help instruction fetch behavior, although in this case it didn’t make a difference. Nevertheless, I’ll do it here because it makes things easier to follow:

Alright, so that’s a nice, sweet, simple loop. Now a lot of people will tell you that out-of-order cores are hard to optimize for since they’re “unpredictable” or “fuzzy” or whatever. I disagree: optimizing for out-of-order cores is *easy* and far less tedious than say manual scheduling for in-order machines is. It’s true that for OoO, you can’t just give a fixed “clock cycles per iteration” number, but the same thing is already true for *anything* with a cache, so who are we kidding? The reality of the situation is that while predicting the exact flow uops are gonna take through the machine is hard (and also fairly pointless unless you’re trying to build an exact pipeline simulator), quantifying the overall statistical behavior of loops on OoO cores is often easier than it is for in-order machines. Because for nice simple loops like this, it boils down to operation counting - total number of instructions, and total amount of work going to different types of functional units. We don’t need to worry about scheduling; the cores can take care of that themselves, and the loop above has no tricky data dependencies between iterations (the only inter-iteration change is the “add ecx, 8″, which doesn’t depend on anything else in the loop) so everything is gonna work fine on that front. So, on to the counting. I’m counting two things here: 1. “fused domain” uops (to a first-order approximation, this means “instructions as broken down by the CPU front-end”) and 2. un-fused uops going to specific groups of functional units (”ports”), which is what the CPU back-end deals with. When I write “unfused p0″, I mean an unfused uop that has to go to port 0. “unfused 1 p23″ is an unfused uop that can go to ports 2 or 3 (whichever happens to be free). I’m using stats for the i7-2600K in my machine (Intel Sandy Bridge); newer CPUs have slightly different (but still similar) breakdowns. Now without further ado, we have:

(yes, the pair of x86 instructions cmp+je combines into one fused uop.)

Fused uops are the currency the CPU frontend deals in. It can process at most 4 of these per cycle, under ideal conditions, although in practice (for various reasons) it’s generally hard to average much more than 3 fused uops/cycle unless the loop is relatively short (which, luckily, this one is). All the ports can accept one instruction per cycle.

So total, we have:

And of that total, the actual box pruning test (the first 5 x86 instructions) are 4 fused uops, 3 unfused p015 and 1 unfused p23 - a single cycle’s worth of work. In other words, we spend more than half of our execution bandwidth on loop overhead. That’s no good.

Hence, unroll 4x. With that, provided there *are* at least 4 boxes to test against in the current cluster, we end up with:

Our bottleneck are once again ports 0,1,5, but they now process 4 candidate pairs in 5.33 cycles worth of work, whereas they took 9.33 cycles worth of work before. So from that analysis, we expect something like a 42.8% reduction in execution time, theoretical. Actual observed reduction was 34.4% on my home i7-2600K (12038 Kcyc -> 7893 Kcyc) and 42.9% on my work i7-3770S (8990 Kcyc -> 5131 Kcyc). So the Sandy Bridge i7-2600K also runs into some other limits not accounted for in this (very simplistic!) analysis whereas the i7-3770S behaves *exactly* as predicted.

The other tweak I tried later was to switch things around so the box X coordinates are converted to integers. The issue is our 2-fused-uop COMISS, which we’d like to replace with a 1-fused-uop compare. Not only is the integer version fewer uops, the CMP uop is also p015 instead of the more constrained p0+p1 for COMISS.

What would we expect from that? Our new totals are:

From the back-of-the-envelope estimate, we now go from purely backend limited to simultaneously backend and frontend limited, and we’d expect to go from about 5.33 cycles/iter to 5 cycles/iter, for a 6.2% reduction.

And indeed, on my work i7-3770S, this change gets us from 5131 Kcyc -> 4762 Kcyc, reducing the cycle count by 7.2%. Close enough, and actually a bit better than expected!

This example happens to work out very nicely (since it has a lot of arithmetic and few branch mispredictions or cache misses), but the same general ideas apply elsewhere. Who says that out-of-order cores are so hard to predict?

—-

Right. Thank you Fabian. That was certainly a… rigorous explanation.

Here are a few comments that come to mind:

• It is certainly true that manually pairing the assembly code for the U and V pipelines of the first Pentiums (which I did a lot in the past) was far more tedious than letting the out-of-order processors deal with it for me.
• It boils down to operation counting indeed. That’s what we noticed in the previous posts: reducing the total number of instructions has a measurable impact on performance in this case.
• I did try to restructure the loop to remove the jump from the hot path, but as you noticed as well it didn’t make any difference. But as a side-effect of another goal (reducing the size of the main loop), the hot path became jump-free in version 14a anyway.
• Using integers is what we tried in version 7 already. While we did measure gains, they were too small to matter and we ignored them. That being said, version 7 took 40000+ KCycles… so the gains might have been small compared to the total cost at the time, but if we still get the same gains today it might be a different story. In other words, going from 5131 to 4762 K-Cycles is just a 369 K-Cycles gain: peanuts compared to 40000, but probably worth it compared to 4000. And yes, using integers for X’s only may also be a better idea than using them for everything. So we will revisit this and see what happens in the C++ version.

In any case, here are the timings for Ryg’s version on my machines:

The Delta and Speedup columns are computed between Ryg’s version and the previous best assembly version. The Timings and Overall X factor columns are absolute values that you can use to compare Ryg’s version to our initial C++ unrolled version (14a). The comparisons are not entirely apple-to-apple:

• Versions 12 and 14b are “unsafe”, version 14a is “safe”.
• Versions 12 and 14b are assembly, version 14a is C++.
• Version 14b does more than unrolling the loop, it also switches some floats to integers.

So the comparisons might not be entirely “fair” but it doesn’t matter: they give a good idea of what kind of performance we can achieve in “ideal” conditions where the compiler doesn’t get in the way.

It gives a target performance number to reach.

And that’s perfect really because we just reached our previous performance target (10x!) in the previous post.

So we need a new one. Perfect timing to send me new timings.

Well, gentlemen, here it is: our new goal is to reach the same performance as Ryg’s unrolled assembly version, but using only C++ / intrinsics – to keep things somewhat portable.

This is what we will try to do next time.

Stay tuned!

What we learnt:

It is always a good idea to make your code public and publish your results. More often than not you get good feedback and learn new things in return. Sometimes you even learn how to make your code go faster.

Ex-scene coders rule. (Well we knew that already, didn’t we?)

GitHub code for part 14b